BFS (너비 우선 탐색)
트리나 그래프를 탐색하는 방법으로 시작 정점에서 가장 가까운 정점을 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 방법이다.
BFS를 구현할 때는 Queue를 활용하는데 왜 Queue를 쓰는지 아래의 과정을 통해 알아보자.
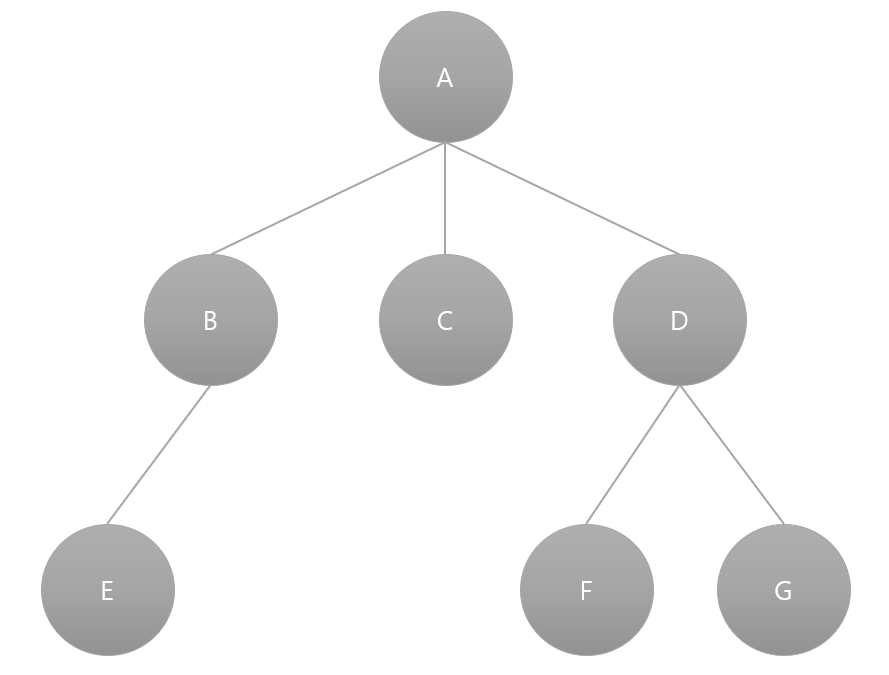
BFS 탐색 과정
1. 루트 노트 방문
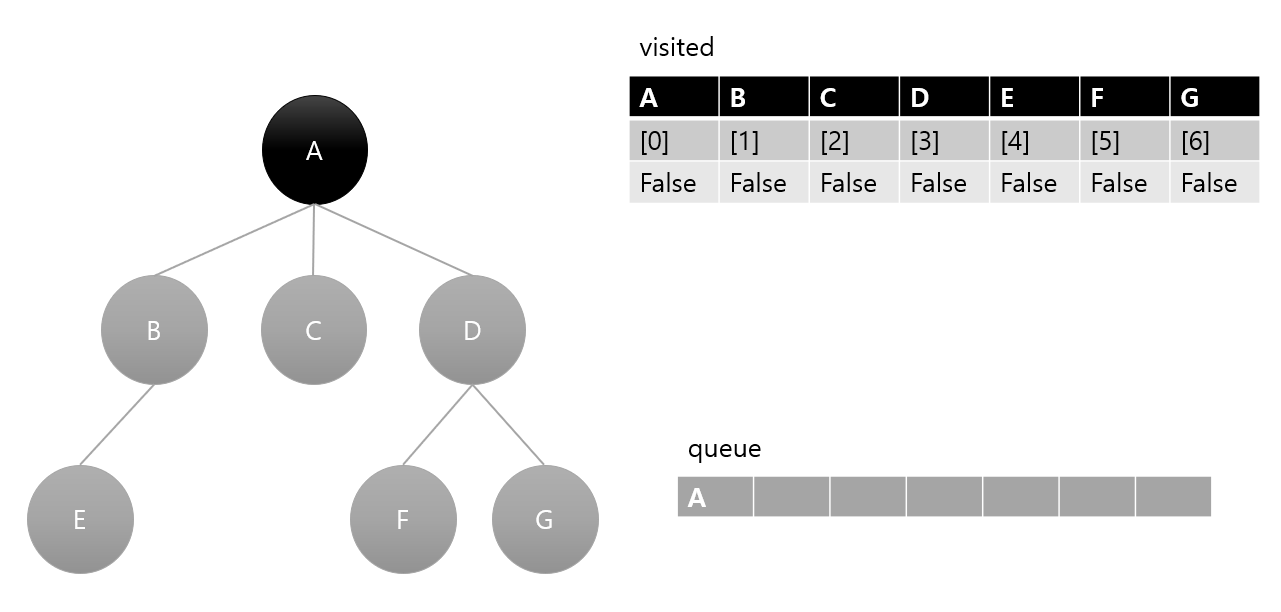
2. 큐에서 A를 제거 후 방문 처리, 다음 인접 노드들 큐에 삽입
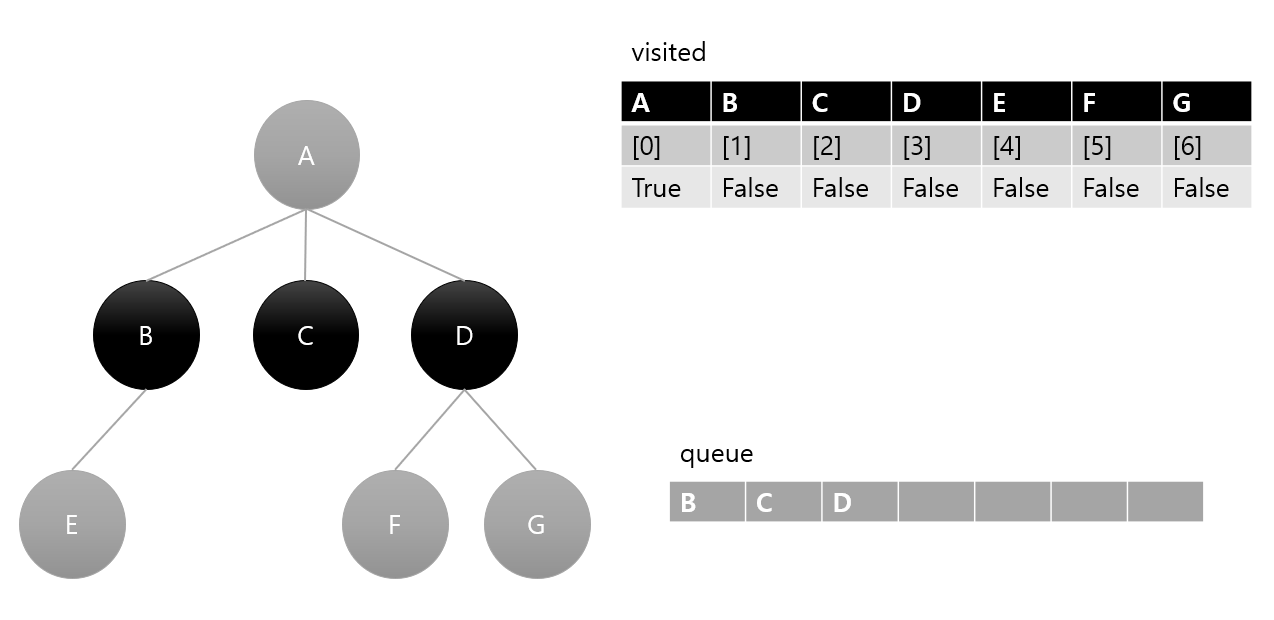
3. queue 에서 요소 하나 pop(B) 후 방문 처리, B의 인접 노드 큐에 삽입
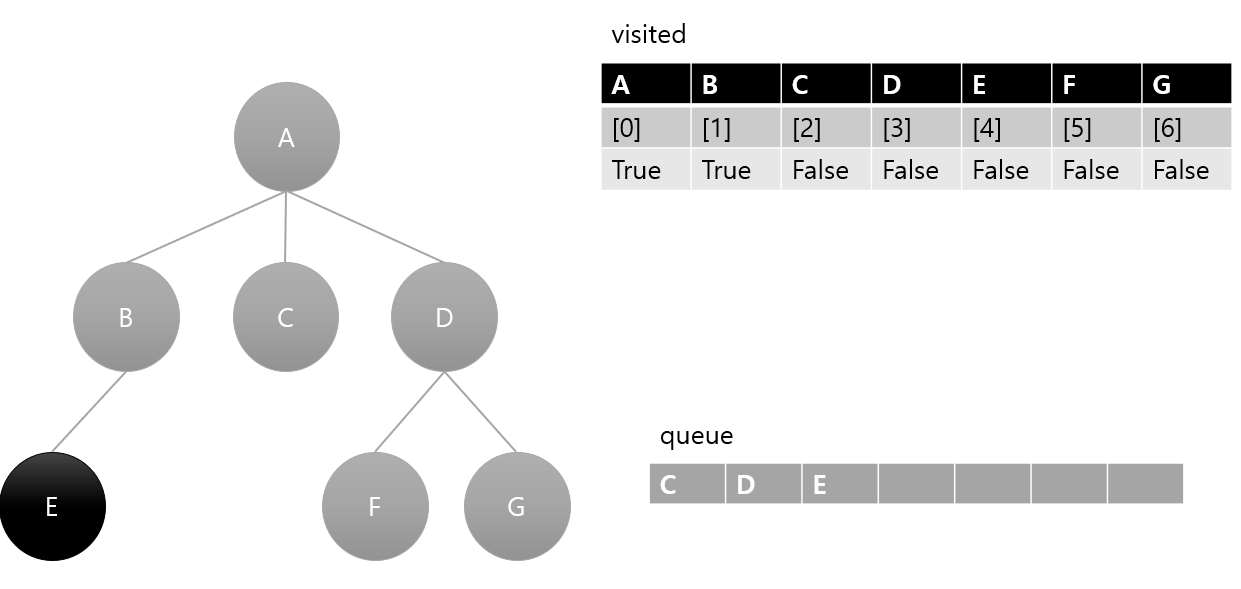
4. queue 에서 요소 하나 pop(C) 후 방문 처리, C의 인접 노드 큐에 삽입
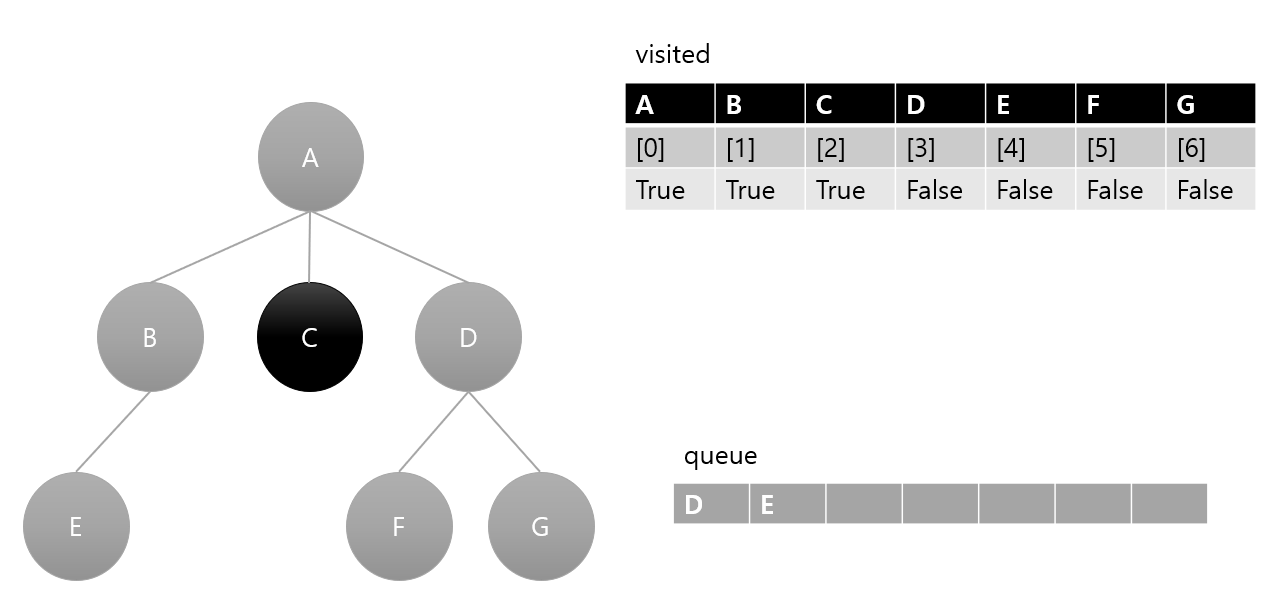
5. queue 에서 요소 하나 pop(D) 후 방문 처리, D의 인접 노드 큐에 삽입
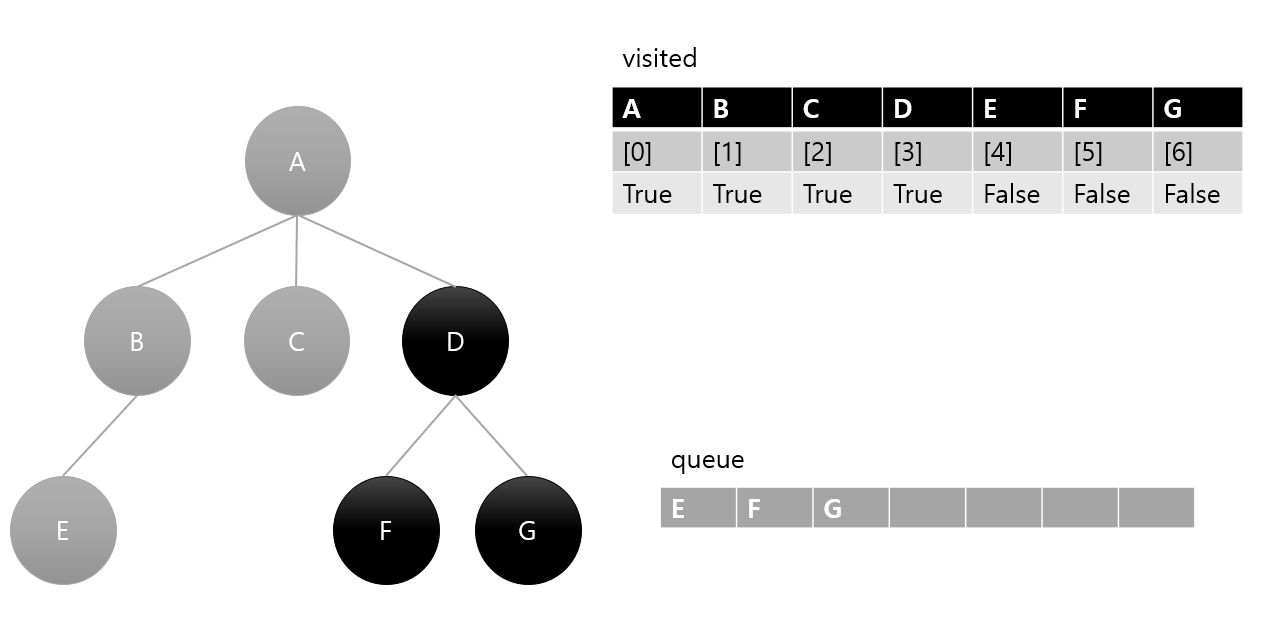
6. queue에서 남아있는 요소들을 위와 같은 방법으로 방문 및 표시하면서 큐가 완전히 비게 된다면 탐색 완료.
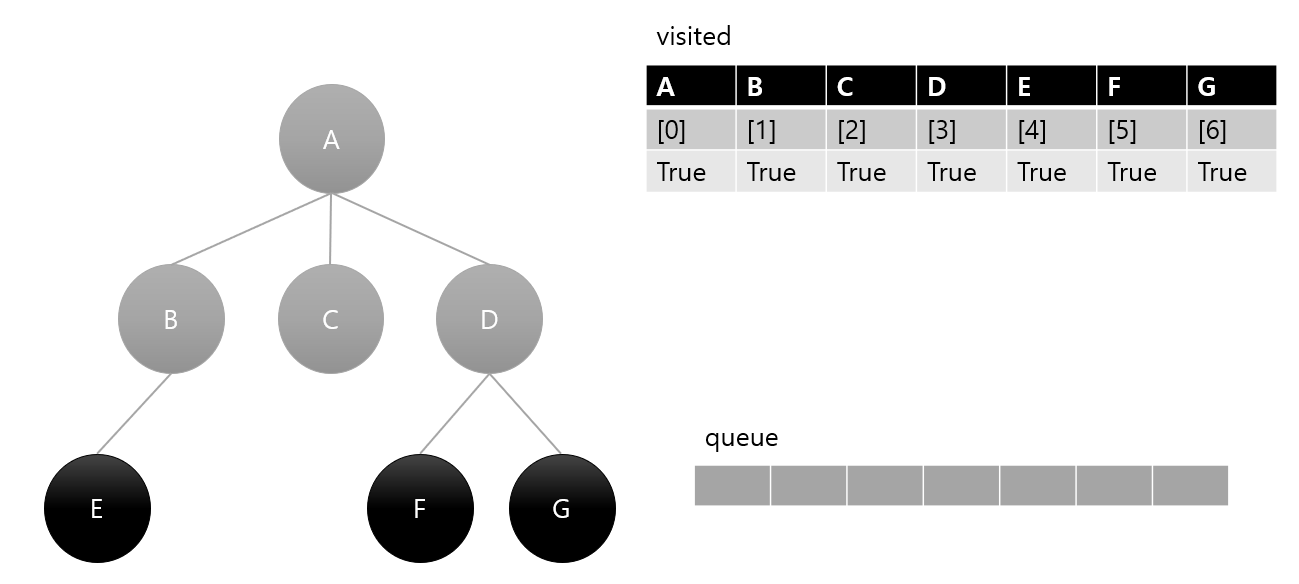
queue에서 pop 한 순서를 정리하면 A -> B -> C -> D -> E -> F -> G 인데 이는 BFS 탐색 결과이다.
이제 Java 코드로 BFS를 구현해보겠다.
Java 코드로 구현
BFS를 구현하기에 앞서 3가지가 선행되어야한다.
- 탐색할 2차원 배열 또는 그래프
- 방문처리를 하기 위한 boolean type
- Queue 자료 구조
이 3가지가 준비되었다면 BFS를 구현할 수 있다.
public static void BFS(int n){
queue.offer(n);
visited[n] = true;
while (!queue.isEmpty()) {
int x = q.poll();
sb.append(x).append(" ");
for (int y : graph[x]) {
if (!visited[y]) {
queue.offer(y);
visited[y] = true;
}
}
}
}반복문을 모두 수행 후 sb를 출력하면 BFS의 탐색 순서가 나온다.
특징
- DFS와의 가장 큰 차이로, 여러 갈래 중 무한한 길이를 가지는 경로가 존재하고 탐색 목표가 다른 경로에 존재하는 경우 DFS로 탐색할 시에는 무한한 길이의 경로에서 영원히 종료하지 못하지만, BFS의 경우는 모든 경로를 동시에 진행하기 때문에 탐색이 가능하다는 특징이 있다.
- 가중치가 없는 그래프에서 출발노드에서 목표노드까지의 최단 길이 경로를 보장한다.
- 재귀호출을 사용하는 DFS와 달리 큐를 이용해 다음에 탐색 할 노드들을 저장하기 때문에 노드의 수가 많을 수록 더 큰 저장공간 필요하다.
DFS(깊이 우선 탐색)
트리나 그래프에서 한 루트로 탐색하다가 특정 상황에서 최대한 깊숙이 들어가서 확인한 뒤 다시 돌아가 다른 루트로 탐색하는 방식이다.
주로 구현 방법은 재귀호출, 스택이며 구조상 스택 오버플로우를 조심해야한다.
DFS 탐색 과정
아래는 그림으로 표현한 DFS의 과정이다.
1. 루트 노드 방문
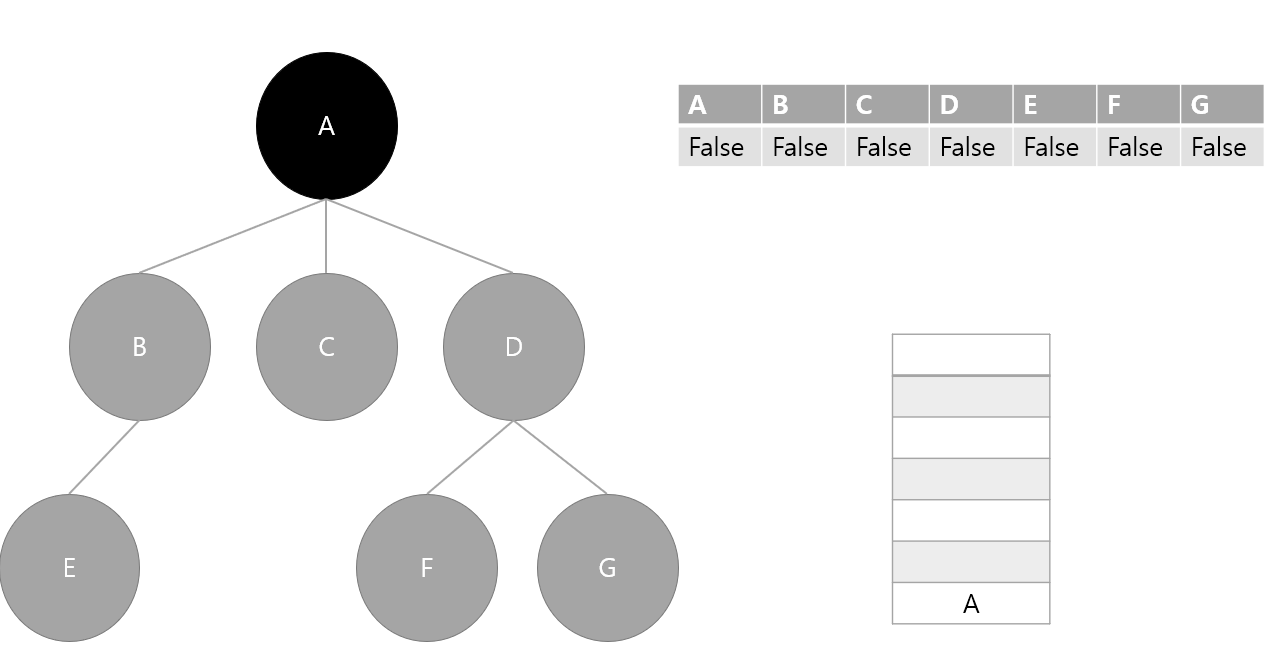
2. 스택에서 A를 제거 후 방문 처리, 다음 인접 노드들 스택에 삽입
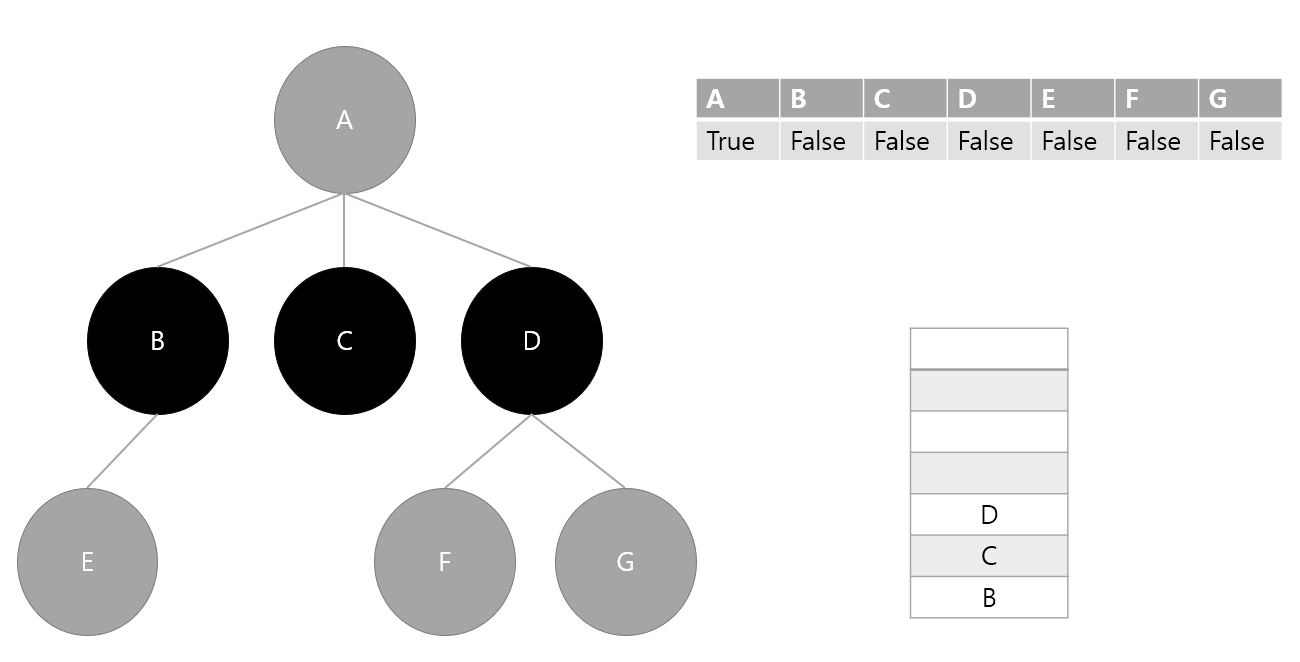
3. 스택에서 요소 하나 pop(D) 후 방문 처리, D의 인접 노드 스택에 삽입
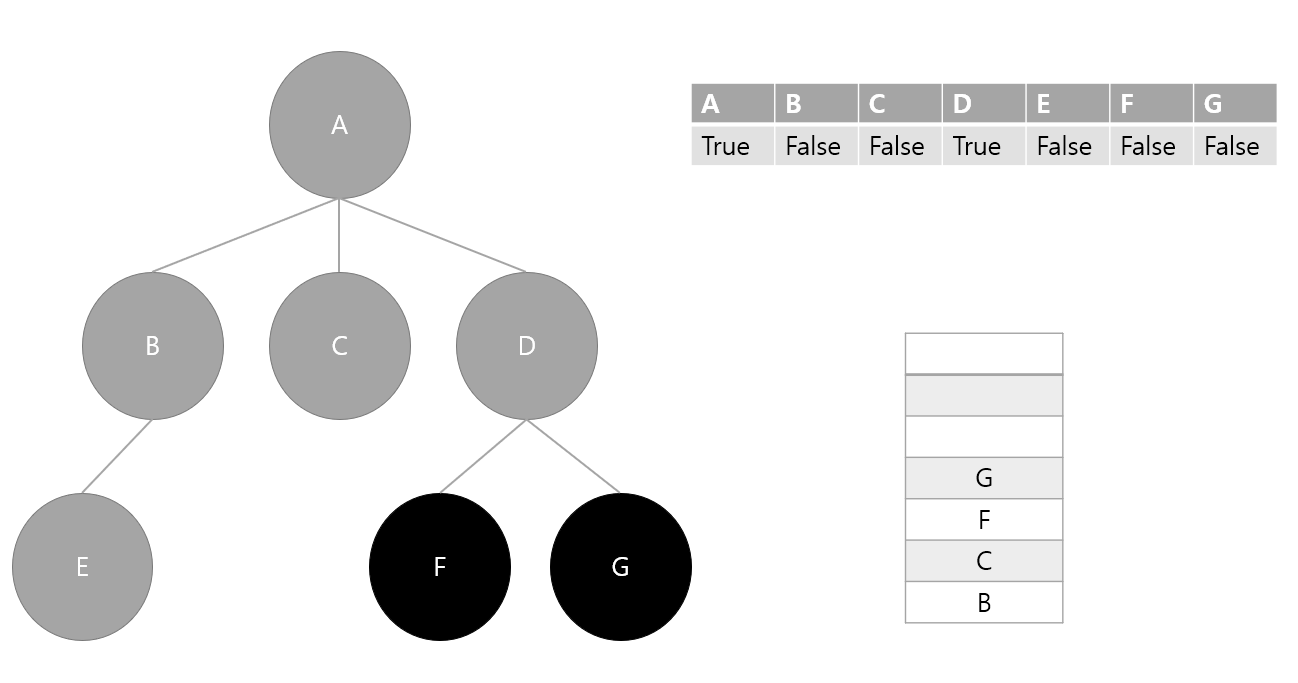
3. 스택에서 요소 하나 pop(G) 후 방문 처리, 인접 노드가 없기 때문에 다음단계로
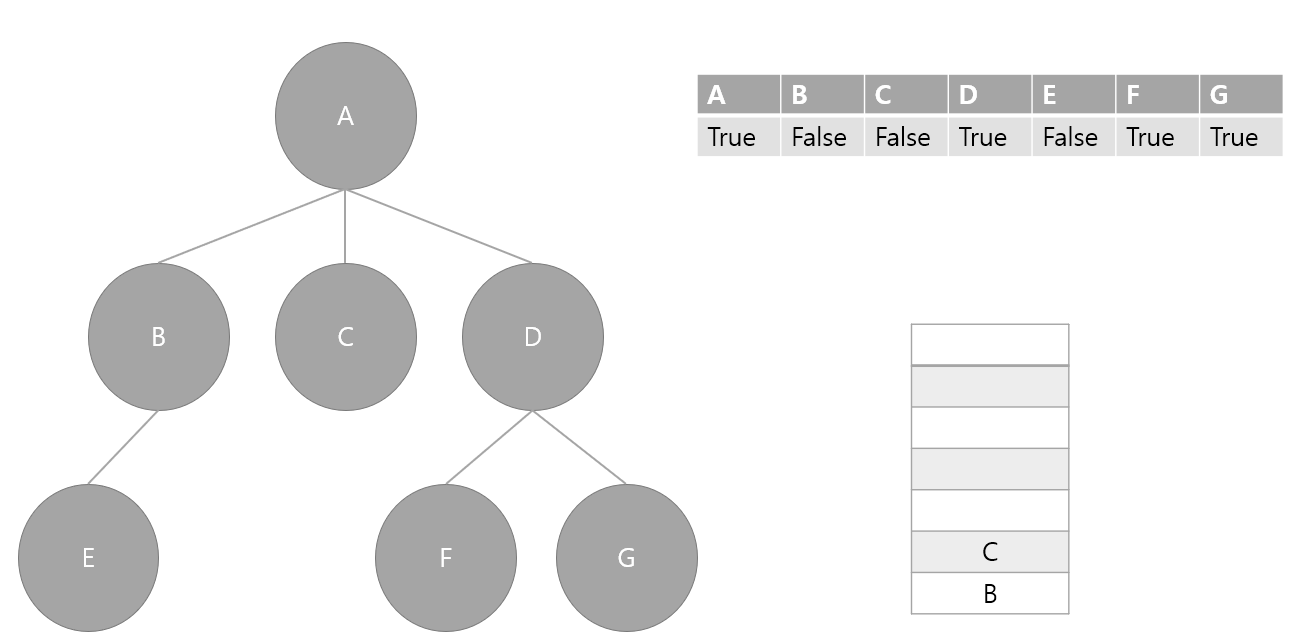
4. 스택에서 요소 하나 pop(C) 후 방문 처리, 인접 노드가 없기 때문에 다음단계로
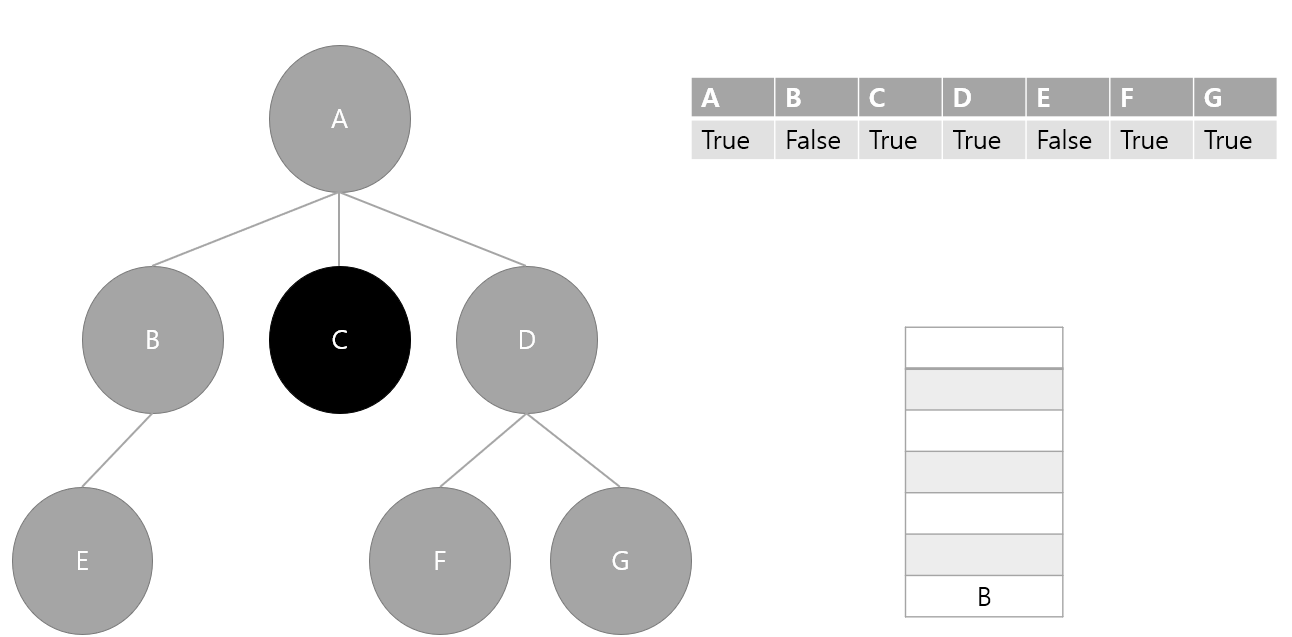
5. 스택에서 요소 하나 pop(B) 후 방문 처리, B의 인접 노드 스택에 삽입
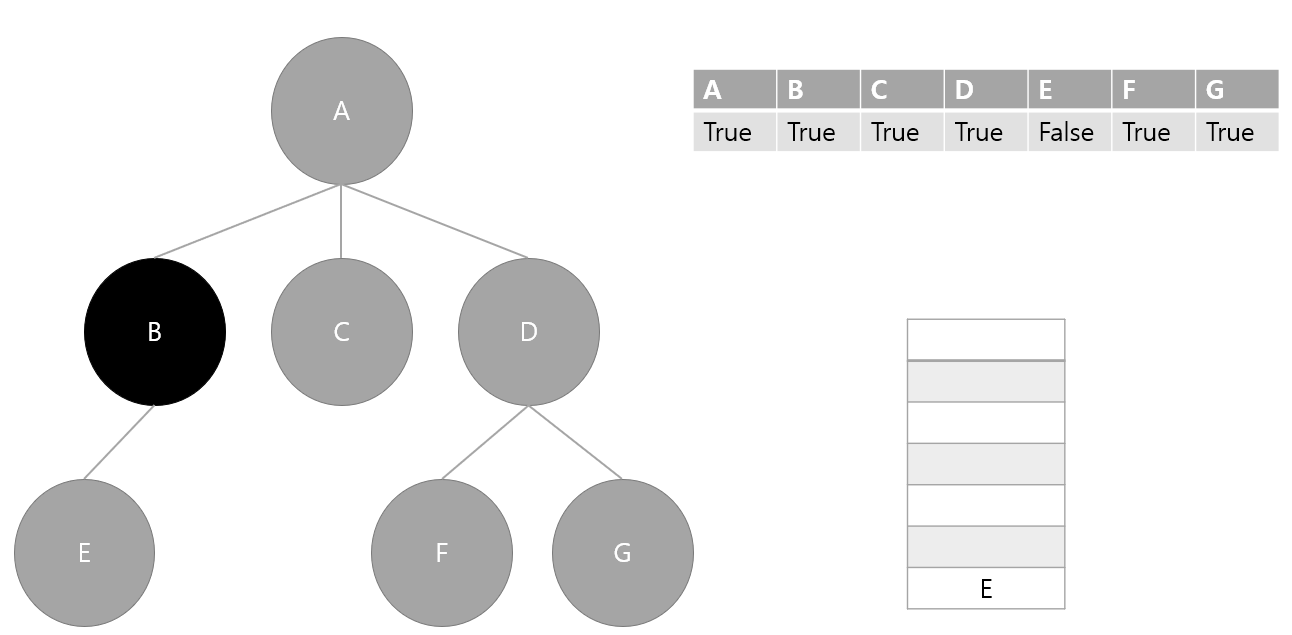
6. 스택에서 요소 하나 pop(E) 후 방문 처리, 스택에서 더 이상 탐색할 요소가 없기 때문에 종료
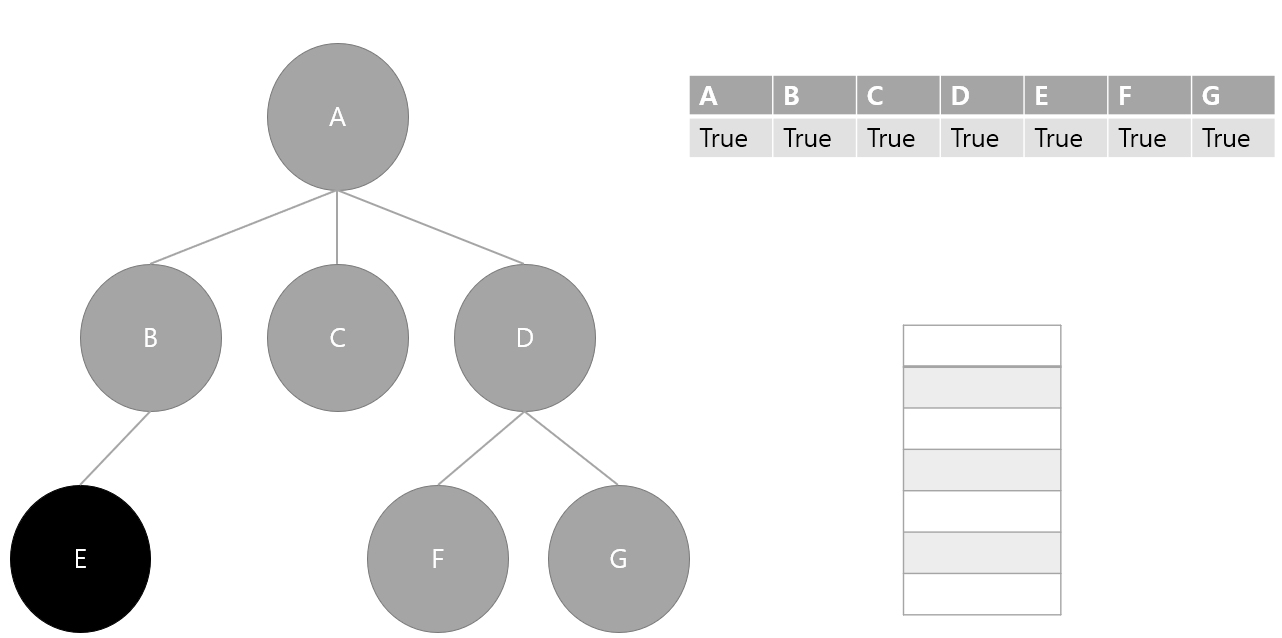
stack에서 pop 한 순서를 정리하면 A -> D -> G -> F -> C -> B -> E 인데 이는 DFS 탐색 결과이다.
이제 Java 코드로 DFS를 구현해보겠다.
Java 코드로 구현
DFS 또한 구현하기에 앞서 3가지가 선행되어야한다.
- 탐색할 2차원 배열 또는 그래프
- 방문처리를 하기 위한 boolean type
- stack 자료 구조 or 재귀
public static void dfs(int x) {
visited[x] = true;
sb.append(x).append(" ");
for (int i = 0; i < graph[x].length; i++) {
if (!visited[graph[x][i]]){
dfs(graph[x][i]);
}
}
}재귀가 모두 수행된 후 sb를 출력하면 DFS의 탐색 순서가 나온다.
특징
- 단지 현 경로상의 노드들만을 기억하면 되므로 저장 공간의 수요가 비교적 적다.
- 목표 노드가 깊은 단계에 있을 경우 해를 빨리 구할 수 있다.
- 해가 없는 경로가 깊다면 깊이 빠질 가능성이 있다.
- 경로가 여러개인 경우 얻어진 해가 최단 경로가 된다는 보장이 없다
'알고리즘' 카테고리의 다른 글
| 순차탐색, 이진탐색, 그래프 (0) | 2022.10.27 |
|---|---|
| 재귀호출, 동적계획법, 분할 정복 (1) | 2022.10.13 |
| 알고리즘 스터디 - 정렬 정리 (0) | 2022.09.29 |
BFS (너비 우선 탐색)
트리나 그래프를 탐색하는 방법으로 시작 정점에서 가장 가까운 정점을 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 방법이다.
BFS를 구현할 때는 Queue를 활용하는데 왜 Queue를 쓰는지 아래의 과정을 통해 알아보자.

BFS 탐색 과정
1. 루트 노트 방문

2. 큐에서 A를 제거 후 방문 처리, 다음 인접 노드들 큐에 삽입

3. queue 에서 요소 하나 pop(B) 후 방문 처리, B의 인접 노드 큐에 삽입

4. queue 에서 요소 하나 pop(C) 후 방문 처리, C의 인접 노드 큐에 삽입

5. queue 에서 요소 하나 pop(D) 후 방문 처리, D의 인접 노드 큐에 삽입

6. queue에서 남아있는 요소들을 위와 같은 방법으로 방문 및 표시하면서 큐가 완전히 비게 된다면 탐색 완료.

queue에서 pop 한 순서를 정리하면 A -> B -> C -> D -> E -> F -> G 인데 이는 BFS 탐색 결과이다.
이제 Java 코드로 BFS를 구현해보겠다.
Java 코드로 구현
BFS를 구현하기에 앞서 3가지가 선행되어야한다.
- 탐색할 2차원 배열 또는 그래프
- 방문처리를 하기 위한 boolean type
- Queue 자료 구조
이 3가지가 준비되었다면 BFS를 구현할 수 있다.
public static void BFS(int n){
queue.offer(n);
visited[n] = true;
while (!queue.isEmpty()) {
int x = q.poll();
sb.append(x).append(" ");
for (int y : graph[x]) {
if (!visited[y]) {
queue.offer(y);
visited[y] = true;
}
}
}
}반복문을 모두 수행 후 sb를 출력하면 BFS의 탐색 순서가 나온다.
특징
- DFS와의 가장 큰 차이로, 여러 갈래 중 무한한 길이를 가지는 경로가 존재하고 탐색 목표가 다른 경로에 존재하는 경우 DFS로 탐색할 시에는 무한한 길이의 경로에서 영원히 종료하지 못하지만, BFS의 경우는 모든 경로를 동시에 진행하기 때문에 탐색이 가능하다는 특징이 있다.
- 가중치가 없는 그래프에서 출발노드에서 목표노드까지의 최단 길이 경로를 보장한다.
- 재귀호출을 사용하는 DFS와 달리 큐를 이용해 다음에 탐색 할 노드들을 저장하기 때문에 노드의 수가 많을 수록 더 큰 저장공간 필요하다.
DFS(깊이 우선 탐색)
트리나 그래프에서 한 루트로 탐색하다가 특정 상황에서 최대한 깊숙이 들어가서 확인한 뒤 다시 돌아가 다른 루트로 탐색하는 방식이다.
주로 구현 방법은 재귀호출, 스택이며 구조상 스택 오버플로우를 조심해야한다.
DFS 탐색 과정
아래는 그림으로 표현한 DFS의 과정이다.
1. 루트 노드 방문

2. 스택에서 A를 제거 후 방문 처리, 다음 인접 노드들 스택에 삽입

3. 스택에서 요소 하나 pop(D) 후 방문 처리, D의 인접 노드 스택에 삽입

3. 스택에서 요소 하나 pop(G) 후 방문 처리, 인접 노드가 없기 때문에 다음단계로

4. 스택에서 요소 하나 pop(C) 후 방문 처리, 인접 노드가 없기 때문에 다음단계로

5. 스택에서 요소 하나 pop(B) 후 방문 처리, B의 인접 노드 스택에 삽입

6. 스택에서 요소 하나 pop(E) 후 방문 처리, 스택에서 더 이상 탐색할 요소가 없기 때문에 종료

stack에서 pop 한 순서를 정리하면 A -> D -> G -> F -> C -> B -> E 인데 이는 DFS 탐색 결과이다.
이제 Java 코드로 DFS를 구현해보겠다.
Java 코드로 구현
DFS 또한 구현하기에 앞서 3가지가 선행되어야한다.
- 탐색할 2차원 배열 또는 그래프
- 방문처리를 하기 위한 boolean type
- stack 자료 구조 or 재귀
public static void dfs(int x) {
visited[x] = true;
sb.append(x).append(" ");
for (int i = 0; i < graph[x].length; i++) {
if (!visited[graph[x][i]]){
dfs(graph[x][i]);
}
}
}재귀가 모두 수행된 후 sb를 출력하면 DFS의 탐색 순서가 나온다.
특징
- 단지 현 경로상의 노드들만을 기억하면 되므로 저장 공간의 수요가 비교적 적다.
- 목표 노드가 깊은 단계에 있을 경우 해를 빨리 구할 수 있다.
- 해가 없는 경로가 깊다면 깊이 빠질 가능성이 있다.
- 경로가 여러개인 경우 얻어진 해가 최단 경로가 된다는 보장이 없다
'알고리즘' 카테고리의 다른 글
| 순차탐색, 이진탐색, 그래프 (0) | 2022.10.27 |
|---|---|
| 재귀호출, 동적계획법, 분할 정복 (1) | 2022.10.13 |
| 알고리즘 스터디 - 정렬 정리 (0) | 2022.09.29 |
