정렬은 사전적 의미로 "물건 등을 가지런히 늘어 세우다" 라는 뜻을 갖고 있다.
우리는 정렬을 왜 할까? 이유는 간단하다. 찾을려고 하는 것을 쉽게 찾고싶어서이다. 즉, 탐색을 위해 정렬을 한다는 것이다.
앞으로 정렬 알고리즘 중 활용도가 높은 버블 정렬, 삽입 정렬, 퀵 정렬 3 가지에 대해 알아볼 예정이고 먼저 버블 정렬(Bubble Sort)부터 소개하겠다.
버블 정렬(Bubble Sort)
버블 정렬은 알고리즘이 데이터를 정렬하는 과정이 마치 물 깊은 곳에서 일어난 거품이 수면을 향해 올라오는 모습과 같다고 해서 붙여진 이름이다.
버블 정렬은 데이터 집합을 순회하면서 집합 내의 이웃 요소들끼리의 교환을 통해 정렬을 수행한다.
이해를 돕기위해 제멋대로 나열되어 있는 수의 집합을 오름차순으로 정렬해보겠다.

버블 정렬은 이웃 요소끼리 교환을 수행한다고 했으니, 교환 전 먼저 둘 사이를 비교하여 이웃끼리 올바른 순서로 위치해 있는지를 확인해야한다. 오름차순으로 정렬하기 때문에 왼쪽 요소가 오른쪽 요소보다 작아야한다.
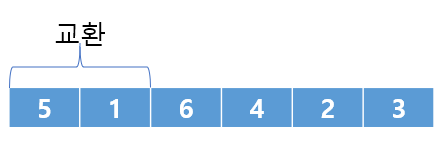

왼쪽이 5이고 오른쪽이 1, 왼쪽의 데이터가 더 크기 때문에 교환을 수행한다. 이후 5, 6은 오름차순으로 돼있기 때문에 다음 요소로 넘어간다. 이런 과정을 배열의 끝까지 진행하면 아래와 같다
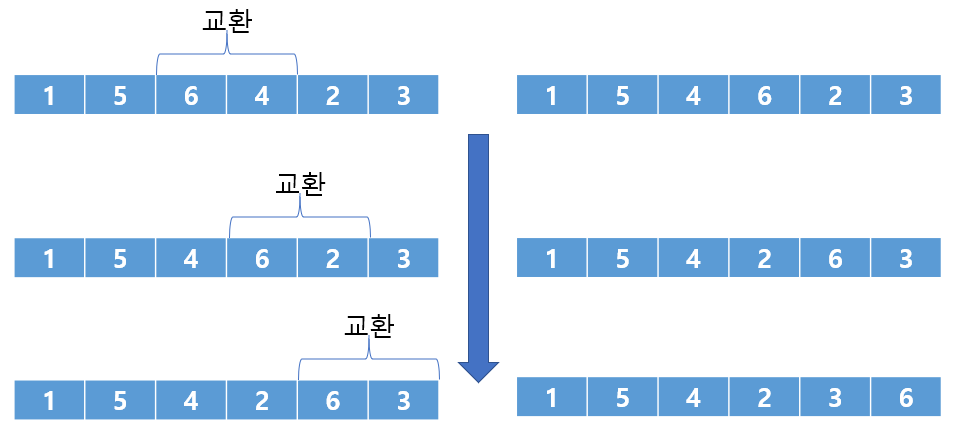
1차적인 과정이 끝나면 6이 오름차순이기 때문에 제일 끝에 간 것을 볼 수 있다. 해당 그림을 세로로 세우면 6이 아래에서 뽀글거리며 올라가는 것처럼 보인다. 그래서 버블정렬이라고 부른다.
6은 정상적인 위치로 갔지만 나머지 숫자들은 아직 정렬되지 않았기 때문에 6을 재외하고 버블정렬을 다시 수행한다.
아래는 2차 버블 정렬 단계를 나타낸 것이다.
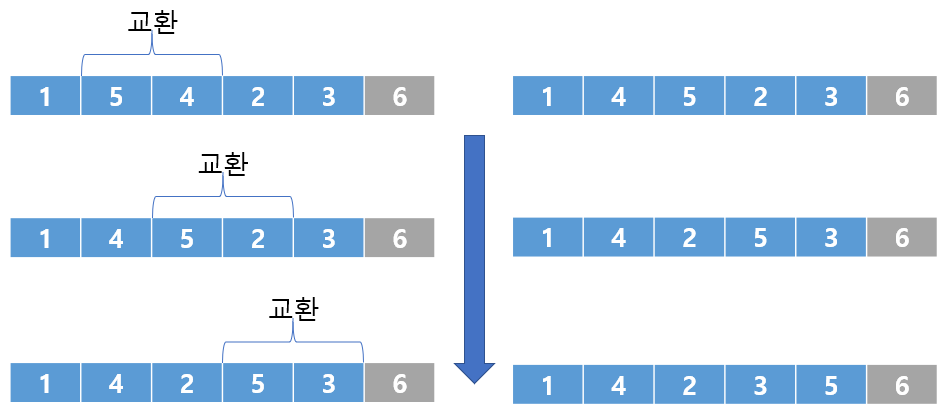
5가 뽀글거리면서 끝으로 간 것을 확인할 수 있다. 이런 과정을 계속 반복하면 아래와 같은 결과를 얻을 수 있다.

아래는 버블 정렬이 대략 어떻게 진행되는지 한눈에 알 수 있는 유튜브 영상이다.
버블 정렬은 얼마나 빠를까?
버블 정렬은 데이터 집합을 한번 순회할 때마다 정렬해야 하는 데이터 집합의 범위가 하나씩 줄어들므로, 데이터 집합의 범위를 n개라고 한다면 n-1만큼 반복하면 정렬이 마무리 된다.
앞에서의 예시를 보면 6이 정렬될때 5개의 요소가 정렬 대상이였고 5가 정렬될때는 4개의 요소가 정렬 대상이였다.
즉, 총 비교 횟수는 5 + 4 + 3 + 2 + 1 = 15 가 된다. 그러면 아래의 식을 도출할 수 있다.
버블 정렬의 비교 횟수 = (n-1) + (n-2) + (n-3) + ... + (n-(n-2)) + (n-(n-1))
=> (n-1) + (n-2) + (n-3) + ... + 2 + 1
=> $$\frac{n(n-1)}{2}$$
이를 통해 시간 복잡도가 O(n²) 가 된다는 것을 알 수 있고 배열 하나만 사용하기 때문에 공간 복잡도는 O(n)이다.
지금은 6개의 데이터라 그렇게 오래 걸린다고 볼 수 없지만 만약 30000개의 데이터를 정렬한다면 대략 450,000,000 회의 비교 연산을 해야함으로 오래 걸린다.
그럼에도 불구하고 버블 정렬을 써야하는 경우는 데이터가 많지 않고 구현이 간단하다면 사용할 수 있을 것이다.
버블 정렬 구현
1차적 스왑 작업 후 다음 단계가 똑같이 진행되기 때문에 이중 for 문으로 구현한다.
점점 진행될수록 비교해야할 배열 크기가 줄어드므로 array.length - (i + 1)로 제약 조건을 설정하였다.
오름차순으로 정렬하기 위해 현재 데이터가 다음 데이터보다 크다면 스왑하도록 구현하였다.
int[] sort()
{
for (int i = 0; i < array.length - 1; i++)
{
for (int j = 0; j < array.length - (i + 1); j++)
{
if(array[j] > array[j + 1])
{
swap(j + 1, j);
}
}
}
return array;
}
void swap(int to, int from)
{
int swap = array[to];
array[to] = array[from];
array[from] = swap;
}정리
- 장점 : 간단한 구현, 데이터를 하나하나 비교하므로 정밀
- 단점 : 데이터를 하나하나 비교하기때문에 데이터량이 많다면 오래 걸린다.
'알고리즘 > 알고리즘' 카테고리의 다른 글
| 퀵정렬(Quick Sort)의 개념 및 구현 (0) | 2022.07.01 |
|---|---|
| 삽입정렬(Insertion Sort)의 개념 및 구현 (0) | 2022.07.01 |
정렬은 사전적 의미로 "물건 등을 가지런히 늘어 세우다" 라는 뜻을 갖고 있다.
우리는 정렬을 왜 할까? 이유는 간단하다. 찾을려고 하는 것을 쉽게 찾고싶어서이다. 즉, 탐색을 위해 정렬을 한다는 것이다.
앞으로 정렬 알고리즘 중 활용도가 높은 버블 정렬, 삽입 정렬, 퀵 정렬 3 가지에 대해 알아볼 예정이고 먼저 버블 정렬(Bubble Sort)부터 소개하겠다.
버블 정렬(Bubble Sort)
버블 정렬은 알고리즘이 데이터를 정렬하는 과정이 마치 물 깊은 곳에서 일어난 거품이 수면을 향해 올라오는 모습과 같다고 해서 붙여진 이름이다.
버블 정렬은 데이터 집합을 순회하면서 집합 내의 이웃 요소들끼리의 교환을 통해 정렬을 수행한다.
이해를 돕기위해 제멋대로 나열되어 있는 수의 집합을 오름차순으로 정렬해보겠다.

버블 정렬은 이웃 요소끼리 교환을 수행한다고 했으니, 교환 전 먼저 둘 사이를 비교하여 이웃끼리 올바른 순서로 위치해 있는지를 확인해야한다. 오름차순으로 정렬하기 때문에 왼쪽 요소가 오른쪽 요소보다 작아야한다.


왼쪽이 5이고 오른쪽이 1, 왼쪽의 데이터가 더 크기 때문에 교환을 수행한다. 이후 5, 6은 오름차순으로 돼있기 때문에 다음 요소로 넘어간다. 이런 과정을 배열의 끝까지 진행하면 아래와 같다

1차적인 과정이 끝나면 6이 오름차순이기 때문에 제일 끝에 간 것을 볼 수 있다. 해당 그림을 세로로 세우면 6이 아래에서 뽀글거리며 올라가는 것처럼 보인다. 그래서 버블정렬이라고 부른다.
6은 정상적인 위치로 갔지만 나머지 숫자들은 아직 정렬되지 않았기 때문에 6을 재외하고 버블정렬을 다시 수행한다.
아래는 2차 버블 정렬 단계를 나타낸 것이다.

5가 뽀글거리면서 끝으로 간 것을 확인할 수 있다. 이런 과정을 계속 반복하면 아래와 같은 결과를 얻을 수 있다.

아래는 버블 정렬이 대략 어떻게 진행되는지 한눈에 알 수 있는 유튜브 영상이다.
버블 정렬은 얼마나 빠를까?
버블 정렬은 데이터 집합을 한번 순회할 때마다 정렬해야 하는 데이터 집합의 범위가 하나씩 줄어들므로, 데이터 집합의 범위를 n개라고 한다면 n-1만큼 반복하면 정렬이 마무리 된다.
앞에서의 예시를 보면 6이 정렬될때 5개의 요소가 정렬 대상이였고 5가 정렬될때는 4개의 요소가 정렬 대상이였다.
즉, 총 비교 횟수는 5 + 4 + 3 + 2 + 1 = 15 가 된다. 그러면 아래의 식을 도출할 수 있다.
버블 정렬의 비교 횟수 = (n-1) + (n-2) + (n-3) + ... + (n-(n-2)) + (n-(n-1))
=> (n-1) + (n-2) + (n-3) + ... + 2 + 1
=> $$\frac{n(n-1)}{2}$$
이를 통해 시간 복잡도가 O(n²) 가 된다는 것을 알 수 있고 배열 하나만 사용하기 때문에 공간 복잡도는 O(n)이다.
지금은 6개의 데이터라 그렇게 오래 걸린다고 볼 수 없지만 만약 30000개의 데이터를 정렬한다면 대략 450,000,000 회의 비교 연산을 해야함으로 오래 걸린다.
그럼에도 불구하고 버블 정렬을 써야하는 경우는 데이터가 많지 않고 구현이 간단하다면 사용할 수 있을 것이다.
버블 정렬 구현
1차적 스왑 작업 후 다음 단계가 똑같이 진행되기 때문에 이중 for 문으로 구현한다.
점점 진행될수록 비교해야할 배열 크기가 줄어드므로 array.length - (i + 1)로 제약 조건을 설정하였다.
오름차순으로 정렬하기 위해 현재 데이터가 다음 데이터보다 크다면 스왑하도록 구현하였다.
int[] sort()
{
for (int i = 0; i < array.length - 1; i++)
{
for (int j = 0; j < array.length - (i + 1); j++)
{
if(array[j] > array[j + 1])
{
swap(j + 1, j);
}
}
}
return array;
}
void swap(int to, int from)
{
int swap = array[to];
array[to] = array[from];
array[from] = swap;
}정리
- 장점 : 간단한 구현, 데이터를 하나하나 비교하므로 정밀
- 단점 : 데이터를 하나하나 비교하기때문에 데이터량이 많다면 오래 걸린다.
'알고리즘 > 알고리즘' 카테고리의 다른 글
| 퀵정렬(Quick Sort)의 개념 및 구현 (0) | 2022.07.01 |
|---|---|
| 삽입정렬(Insertion Sort)의 개념 및 구현 (0) | 2022.07.01 |
