퀵정렬(Quick Sort)이란?
퀵정렬은 분할정복에 기반한 알고리즘이다. 분할정복이란 전체를 공략하는 대신 전체를 구성하는 구성 요소들을 나누어 잘게 쪼개진 적을 공략하는 개념이다.
퀵 정렬은 아래와 같은 과정으로 분할 정복을 이용해 정렬을 한다.
- 데이터 집합 내에서 임의의 기준 요소를 선택하고, 기준 요소보다 작은 요소들은 순서에 관계없이 무조건 기준 요소의 왼편에, 큰 값은 오른편에 위치시킨다.
- 1에서 나눈 데이터 집합들을 다시 1처럼 임의의 기준 요소를 선택하고 같은 방법으로 데이터 집합을 분할한다.
- 1,2 과정을 더 이상 데이터 집합을 나눌 수 없을 때까지 반복하면 정렬된 데이터 집합을 얻는다.
이를 토대로 예시를 들어보겠다.
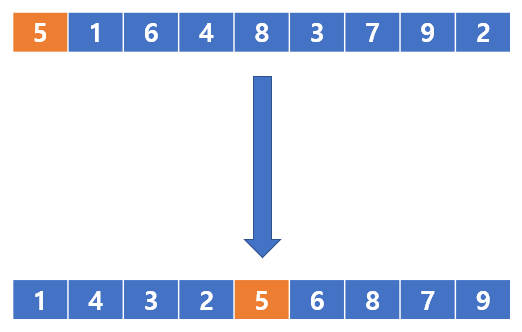
요소 5를 기준으로, 5보다 작은 요소는 왼쪽, 5보다 큰 요소는 오른쪽에 모은다. 결과로 왼쪽과 오른쪽은 정렬되어있지않지만 범위가 한정되어 있는 데이터 집합이 생긴다.
이렇게 생긴 왼쪽과 오른쪽의 데이터 집합에 대해 분할을 수행한다.
우선 왼쪽부터 진행해보겠다.
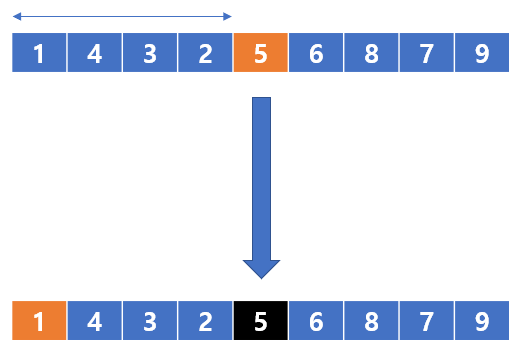
왼쪽부터 1를 기준으로 삼았을때 1의 오른쪽에는 1보다 큰 값들만 있으니 이미 분할되어있다고 볼 수 있다. 따라서 바로 다음 4, 3, 2에 대해 분할을 수행한다.

4를 기준으로 했을때 3, 2 는 4보다 작으므로 4 왼쪽에 위치해야한다. 3, 2 요소들을 옮긴 후 3,2 에 대해 분할을 수행한다.

3을 기준으로 2는 3의 왼쪽에 있어야하기 때문에 해당 위치로 이동시킨다. 이렇게 되면 왼쪽 데이터 집합은 모두 정렬된 것이다. 오른쪽 데이터 집합도 분할을 수행하면 아래와 같다.

분할 결과 이제 완전히 정렬된 데이터 집합을 얻게 되었다.
아래는 퀵 정렬이 대략 어떻게 진행되는지 한눈에 알 수 있는 유튜브 영상이다.
퀵 정렬이 퀵 정렬을 호출한다
퀵 정렬을 구현하기에 앞서 2 가지 의문점이 생긴다.
- 배열을 데이터 집합의 자료구조로 사용할 때, 분할은 어떻게 수행하는가?
- 반복되는 분할 과정을 어떻게 처리할 것인가?
첫번째 문제는 링크드리스트 처럼 삽입/삭제가 자유롭지 때문에 분할 하는 로직이 필요하다.
여기서 피봇이라는 개념을 사용한다. 피봇은 마치 정찰병을 투입하는것과 같습니다. 정찰병 2명을 투입해서 한 명은 왼쪽부터 오른쪽으로 데이터 집합을 검사하면서 기준보다 큰 요소를 찾고, 또 한 명은 반대방향으로 검사하면서 기준보다 작은 요소를 찾는다. 찾은 후에는 서로의 요소를 교환하는 것이다.
그리고 정찰병들이 서로 접선할때까지 해당 행동을 계속 수행한다.

이로써 첫번째 문제는 해결되었다.
두번째 문제의 요지는 "반복되는 분할 과정을 어떻게 프로그래밍 하느냐" 인데 반복되는 동일한 과정이기 때문에 재귀 호출을 사용하면 된다.
이를 바탕으로 퀵정렬을 코드로 구현해보자.
퀵정렬 구현
public int[] sort() {
quickSort(0 , array.length - 1);
return array;
}
private int partition(int left, int right)
{
int first = left;
int pivot = array[first];
++left;
while(left <= right)
{
while (left <= right && array[left] <= pivot) ++left;
while (left <= right && array[right] > pivot) --right;
if (left <= right)
swap(left,right);
}
swap(first,right);
return right;
}
private void quickSort(int left, int right)
{
if(left < right)
{
int index = partition(left, right);
quickSort(left, index - 1);
quickSort(index + 1, right);
}
}분할 역할을 해주는 partition 메소드와 분할 한 값을 토대로 quicksort를 재귀호출하여 퀵정렬을 구현한 모습이다.
partition 메소드에서 중요한 것은 피봇과 비교해 값을 찾는 while문에서 left <= right 조건이 존재해야한다는 것이다.
해당 조건이 없다면 무한이 left나 right가 증감하여 index을 벗어나게 된다.
또한 left <= right 조건에 만족할때만 스왑을 해줘야한다.
퀵 정렬의 성능
이번에는 퀵 정렬의 성능을 한 번 알아보겠다. 퀵 정렬은 재귀 호출 깊이, 데이터 집합을 나누기 위한 비교 횟수가 성능에 영향을 미친다.
퀵 정렬에도 최선의 경우와 최악의 경우가 존재하며 평균적인 경우도 알아보자.
최선의 경우
퀵정렬은 미리 정렬되어 있거나 또는 역순으로 정렬되어 있는것보다 데이터 요소들이 이리저리 흩어져 있을 때 최고의 성능을 보인다.
하지만 이 경우는 로또 1등에 당첨될 확률보다 더 만나기 어려운 경우라고 한다.

그림처럼 각 분할이 1/2로 계속 쪼개진다면 퀵 정렬은 최고의 성능을 보여준다. 4개의 조각을 얻기 위해서 2회 재귀 호출을 해야하고 8개를 얻기 위해서는 3회 호출해야한다. 16개를 얻기 위해선 4회 호출을 한다. 이렇게 우리는 한 가지 규칙을 찾을 수 있는데 퀵정렬의 재귀 호출 깊이는 log2n 이라는 것을 알 수 있다.
이제 비교 횟수를 알아보자. 재귀 호출 첫 단계에는 n회 비교한다. 두번째에는 n/2 + n/2 이므로 n회이다.
세번째에는 n/4 + n/4 + n/4 + n/4 = n회 이다.
따라서 최고의 경우 퀵 정렬의 성능은 아래와 같다.
재귀 호출의 깊이 X 각 재귀 호출 단계에서의 비교 횟수
= n X log2n = nlog2n
즉, 시간 복잡도는 O(log2n) 인 것이다. 공간 복잡도는 배열 하나만 쓰기 때문에 O(n) 이다.
최악의 경우
퀵 정렬의 최악의 경우는 아래의 그림과 같다.

최악인 경우, 각 재귀 호출마다 데이터 집합의 분할이 1 : n - 1으로 이루어진다. 이렇게 되면 재귀호출 깊이는 n - 1이 된다.
재귀호출 마다 범위가 1이 줄어들기 때문이다. 따라서 비교 횟수는 아래와 같다.
(n-1) + (n-2) + (n-3) + ... + 2 + 1 = n(n−1)/2 =>
$$\frac{n(n-1)}{2}$$
이는 버블 정렬, 삽입 정렬의 성능과 똑같다. 하지만 이런 경우는 최선의 경우처럼 아주 드물게 나온다.
평균의 경우
퀵 정렬은 평균적으로 1.39nlog2n 회 비교 수행한다고 한다. 최선의 경우에 비해 39% 정도 느린 것이다.
정리
장점 : 타 정렬에 비해 속도가 빠르다.
단점 : 정렬된 배열에서는 오히려 성능이 떨어진다.
'알고리즘 > 알고리즘' 카테고리의 다른 글
| 삽입정렬(Insertion Sort)의 개념 및 구현 (0) | 2022.07.01 |
|---|---|
| 버블정렬(Bubble Sort)의 개념 및 구현 (0) | 2022.06.30 |
퀵정렬(Quick Sort)이란?
퀵정렬은 분할정복에 기반한 알고리즘이다. 분할정복이란 전체를 공략하는 대신 전체를 구성하는 구성 요소들을 나누어 잘게 쪼개진 적을 공략하는 개념이다.
퀵 정렬은 아래와 같은 과정으로 분할 정복을 이용해 정렬을 한다.
- 데이터 집합 내에서 임의의 기준 요소를 선택하고, 기준 요소보다 작은 요소들은 순서에 관계없이 무조건 기준 요소의 왼편에, 큰 값은 오른편에 위치시킨다.
- 1에서 나눈 데이터 집합들을 다시 1처럼 임의의 기준 요소를 선택하고 같은 방법으로 데이터 집합을 분할한다.
- 1,2 과정을 더 이상 데이터 집합을 나눌 수 없을 때까지 반복하면 정렬된 데이터 집합을 얻는다.
이를 토대로 예시를 들어보겠다.

요소 5를 기준으로, 5보다 작은 요소는 왼쪽, 5보다 큰 요소는 오른쪽에 모은다. 결과로 왼쪽과 오른쪽은 정렬되어있지않지만 범위가 한정되어 있는 데이터 집합이 생긴다.
이렇게 생긴 왼쪽과 오른쪽의 데이터 집합에 대해 분할을 수행한다.
우선 왼쪽부터 진행해보겠다.

왼쪽부터 1를 기준으로 삼았을때 1의 오른쪽에는 1보다 큰 값들만 있으니 이미 분할되어있다고 볼 수 있다. 따라서 바로 다음 4, 3, 2에 대해 분할을 수행한다.

4를 기준으로 했을때 3, 2 는 4보다 작으므로 4 왼쪽에 위치해야한다. 3, 2 요소들을 옮긴 후 3,2 에 대해 분할을 수행한다.

3을 기준으로 2는 3의 왼쪽에 있어야하기 때문에 해당 위치로 이동시킨다. 이렇게 되면 왼쪽 데이터 집합은 모두 정렬된 것이다. 오른쪽 데이터 집합도 분할을 수행하면 아래와 같다.

분할 결과 이제 완전히 정렬된 데이터 집합을 얻게 되었다.
아래는 퀵 정렬이 대략 어떻게 진행되는지 한눈에 알 수 있는 유튜브 영상이다.
퀵 정렬이 퀵 정렬을 호출한다
퀵 정렬을 구현하기에 앞서 2 가지 의문점이 생긴다.
- 배열을 데이터 집합의 자료구조로 사용할 때, 분할은 어떻게 수행하는가?
- 반복되는 분할 과정을 어떻게 처리할 것인가?
첫번째 문제는 링크드리스트 처럼 삽입/삭제가 자유롭지 때문에 분할 하는 로직이 필요하다.
여기서 피봇이라는 개념을 사용한다. 피봇은 마치 정찰병을 투입하는것과 같습니다. 정찰병 2명을 투입해서 한 명은 왼쪽부터 오른쪽으로 데이터 집합을 검사하면서 기준보다 큰 요소를 찾고, 또 한 명은 반대방향으로 검사하면서 기준보다 작은 요소를 찾는다. 찾은 후에는 서로의 요소를 교환하는 것이다.
그리고 정찰병들이 서로 접선할때까지 해당 행동을 계속 수행한다.

이로써 첫번째 문제는 해결되었다.
두번째 문제의 요지는 "반복되는 분할 과정을 어떻게 프로그래밍 하느냐" 인데 반복되는 동일한 과정이기 때문에 재귀 호출을 사용하면 된다.
이를 바탕으로 퀵정렬을 코드로 구현해보자.
퀵정렬 구현
public int[] sort() {
quickSort(0 , array.length - 1);
return array;
}
private int partition(int left, int right)
{
int first = left;
int pivot = array[first];
++left;
while(left <= right)
{
while (left <= right && array[left] <= pivot) ++left;
while (left <= right && array[right] > pivot) --right;
if (left <= right)
swap(left,right);
}
swap(first,right);
return right;
}
private void quickSort(int left, int right)
{
if(left < right)
{
int index = partition(left, right);
quickSort(left, index - 1);
quickSort(index + 1, right);
}
}분할 역할을 해주는 partition 메소드와 분할 한 값을 토대로 quicksort를 재귀호출하여 퀵정렬을 구현한 모습이다.
partition 메소드에서 중요한 것은 피봇과 비교해 값을 찾는 while문에서 left <= right 조건이 존재해야한다는 것이다.
해당 조건이 없다면 무한이 left나 right가 증감하여 index을 벗어나게 된다.
또한 left <= right 조건에 만족할때만 스왑을 해줘야한다.
퀵 정렬의 성능
이번에는 퀵 정렬의 성능을 한 번 알아보겠다. 퀵 정렬은 재귀 호출 깊이, 데이터 집합을 나누기 위한 비교 횟수가 성능에 영향을 미친다.
퀵 정렬에도 최선의 경우와 최악의 경우가 존재하며 평균적인 경우도 알아보자.
최선의 경우
퀵정렬은 미리 정렬되어 있거나 또는 역순으로 정렬되어 있는것보다 데이터 요소들이 이리저리 흩어져 있을 때 최고의 성능을 보인다.
하지만 이 경우는 로또 1등에 당첨될 확률보다 더 만나기 어려운 경우라고 한다.

그림처럼 각 분할이 1/2로 계속 쪼개진다면 퀵 정렬은 최고의 성능을 보여준다. 4개의 조각을 얻기 위해서 2회 재귀 호출을 해야하고 8개를 얻기 위해서는 3회 호출해야한다. 16개를 얻기 위해선 4회 호출을 한다. 이렇게 우리는 한 가지 규칙을 찾을 수 있는데 퀵정렬의 재귀 호출 깊이는 log2n 이라는 것을 알 수 있다.
이제 비교 횟수를 알아보자. 재귀 호출 첫 단계에는 n회 비교한다. 두번째에는 n/2 + n/2 이므로 n회이다.
세번째에는 n/4 + n/4 + n/4 + n/4 = n회 이다.
따라서 최고의 경우 퀵 정렬의 성능은 아래와 같다.
재귀 호출의 깊이 X 각 재귀 호출 단계에서의 비교 횟수
= n X log2n = nlog2n
즉, 시간 복잡도는 O(log2n) 인 것이다. 공간 복잡도는 배열 하나만 쓰기 때문에 O(n) 이다.
최악의 경우
퀵 정렬의 최악의 경우는 아래의 그림과 같다.

최악인 경우, 각 재귀 호출마다 데이터 집합의 분할이 1 : n - 1으로 이루어진다. 이렇게 되면 재귀호출 깊이는 n - 1이 된다.
재귀호출 마다 범위가 1이 줄어들기 때문이다. 따라서 비교 횟수는 아래와 같다.
(n-1) + (n-2) + (n-3) + ... + 2 + 1 = n(n−1)/2 =>
$$\frac{n(n-1)}{2}$$
이는 버블 정렬, 삽입 정렬의 성능과 똑같다. 하지만 이런 경우는 최선의 경우처럼 아주 드물게 나온다.
평균의 경우
퀵 정렬은 평균적으로 1.39nlog2n 회 비교 수행한다고 한다. 최선의 경우에 비해 39% 정도 느린 것이다.
정리
장점 : 타 정렬에 비해 속도가 빠르다.
단점 : 정렬된 배열에서는 오히려 성능이 떨어진다.
'알고리즘 > 알고리즘' 카테고리의 다른 글
| 삽입정렬(Insertion Sort)의 개념 및 구현 (0) | 2022.07.01 |
|---|---|
| 버블정렬(Bubble Sort)의 개념 및 구현 (0) | 2022.06.30 |
