스택이란
스택은 뭔가를 아래에서부터 위로 쌓아 얹어 올리도록 하는 자료구조이다.
스택은 오직 top에서 삭제, 추가가 이루어지기 때문에 중간 인덱스에 데이터 변경을 할 수 없다. 특정위치의 데이터를 추가/삭제 하고싶다면 해당 위치까지 pop을 해야한다.
따라서 스택은 가장 마지막에 들어간 데이터가 제일 먼저 나오고(Last In - First Out) 가장 먼저 들어간 데이터는 가장 나중에 나오게(First In - Last Out)된다.
스택의 주요 기능
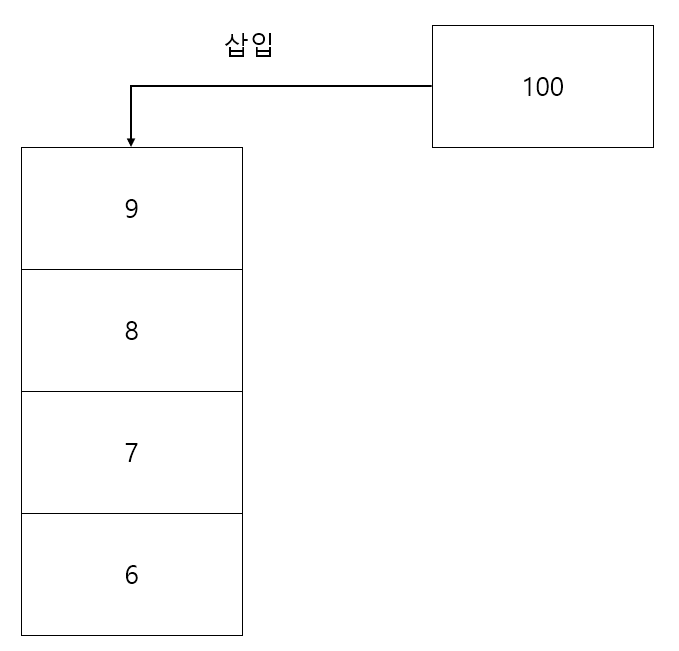
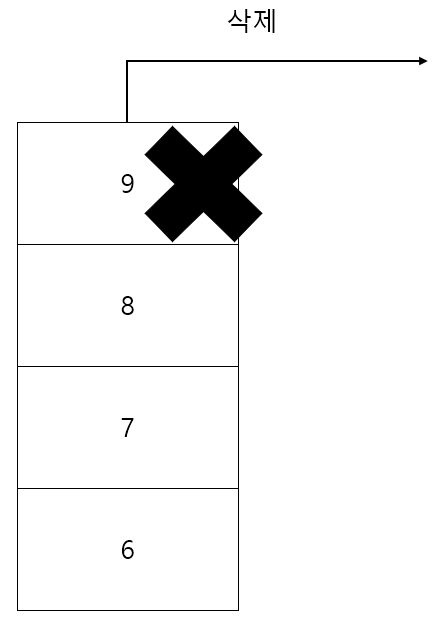
- 삽입
- 제거
스택의 대표적인 기능은 위와 같이 2가지 연산이 있다. 먼저 삽입은 스택 위에 새로운 요소를 쌓는 작업이다.
제거는 스택에서 최상위 요소를 걷어내는 작업이다.
스택 구현 방식
스택을 구현하는 방식으로는 아래와 같이 2가지가 있다
- 배열을 이용
- 링크드리스트를 이용
배열방식은 구현방식이 간단하지만 동적으로 스택 용량 조절이 어렵다는 단점이 있다.
링크드리스트는 구현방식이 배열에 비해 까다롭지만 스택 용량 조절이 동적으로 가능하다는 장점이 존재한다.
배열로 구현하는 스택
배열 기반의 스택은 스택 생성 초기 사용자가 부여한 크기만큼의 데이터 공간을 한꺼번에 생성한다. 그리고 최상위 노드의 위치를 나타내는 변수(Top)를 이용하여 삽입과 제거 연산을 수행한다.
스택이 가지고 있어야할 기본 변수는 최상위 노드의 위치(Top), 배열, 배열의 크기이다.
int capacity;
int top;
Object[] data;스택의 생성
public ArrayStack(int capacity)
{
this.capacity = capacity;
this.top = 0;
this.data = new Object[capacity];
}생성자를 통해 배열의 크기를 capacity에 저장하고 최상위 노드의 위치를 가리킬 Top은 0으로 초기화한다.
Top은 노드가 쌓일 때마다 +1, 삭제될 때마다 -1이 된다.
삽입연산
void push(T data)
{
this.data[top++] = data;
}데이터가 삽입되면 최상위 노드위치(Top)에 데이터를 넣은 후 Top을 증가시킨다.
제거연산
Object pop()
{
data[top] = null;
return data[--top];
}삭제시에는 Top을 감소시킨후 헤당 배열 값을 반환하면 됩니다. 이때 Top이 갖고 있는 값은 실제 최상위 노드가 배열 내에서 위치하는 인덱스 값보다 1만큼 크다는것이다.
크기계산
int getSize()
{
return top;
}스택의 크기는 top을 반환하면 된다. top은 스택의 노드가 추가될때마다 +1이 되기 때문에 이는 크기를 뜻하기도 한다.
빈값체크
boolean isEmpty()
{
return (top == 0);
}top이 0이란 것은 스택에 아무것도 없다는 의미이기 때문에 true를 반환하면 된다.
링크드 리스트로 구현하는 스택
링크드리스트로 구현을 하면 스택의 용량에 제한을 두지 않아도 된다. 그리고 노드는 자신의 위에 위치하는 노드에 대한 포인터를 갖고 있어야 한다. 노드의 구조는 아래와 같다.
class Node
{
private T data;
private Node nextNode;
public Node(T data) {
this.data = data;
this.nextNode = null;
}
public T getData() {
return data;
}
}링크드리스트 스택은 배열기반 스택과는 달리 스택의 용량, 최상위 노드의 인덱스가 없다. 대신 링크드리스트의 헤드(List)와 테일(Top)이 존재한다.
Node List;
Node Top;List는 스택이 기반하고 있는 링크드 리스트에 접근할 수 있게 하고 Top 포인터는 링크드 리스트의 테일을 가리킴으로써 최상위 노드에 대한 정보를 유지한다.
스택의 생성
스택생성 시에는 List, Top 만 생성하기때문에 기본 생성자를 사용한다.
스택에 노드를 삽입할때 노드는 data만 설정하고 nextnode는 null 인 상태로 나둔다.
Node newNode = new Node(newData);삽입연산
이 연산은 링크드리스트의 추가 연산과 비슷하다. 먼저 최상위 노드(Top)을 찾은 다음, 여기에 새 노드를 얹기만 하면 된다. 그런다음 Top은 새 노드를 가리키게 한다.
void push(T newData)
{
Node newNode = new Node(newData);
if(List == null)
{
List = newNode;
}
else
{
Node oldTop = List;
while(oldTop.nextNode != null)
{
oldTop = oldTop.nextNode;
}
oldTop.nextNode = newNode;
}
Top = newNode;
}삽입할때 스택이 빈 경우와 비지않은 경우를 고려해야한다.
제거연산
제거는 아래와 같이 수행된다
- 현재 최상위 노드(Top)를 다른 변수에 복사해둔다
- 현재 최상위 노드의 바로 이전 노드를 찾는다.
- Top을 찾은 이전 노드로 바꾼다.
- 복사해준 옛 최상위 노드를 반환한다.
Node pop()
{
Node TopNode = Top;
if (List == Top)
{
List = null;
Top = null;
}
else
{
Node currentTop = List;
while(currentTop != null && currentTop.nextNode != Top)
{
currentTop = currentTop.nextNode;
}
Top = currentTop;
currentTop.nextNode = null;
}
return TopNode;
}크기계산
링크드리스트의 크기계산과 동일하며 헤드부터 순회하며 count 한다.
int getSize()
{
int count = 0;
Node current = List;
while(current != null)
{
current = current.nextNode;
count++;
}
return count;
}빈값체크
헤드(List) 값이 null라면 데이터가 없는 것이기 때문에 null일때 true를 반환한다.
boolean isEmpty()
{
return (List == null);
}요약
이렇게 구현해봄으로써 알 수 있는 장단점으로는
장점
- top 을 통해 접근하기 때문에 데이터 삽입, 삭제가 빠르다
단점
- top 위치 이외의 데이터에 접근하려면 모든 데이터를 꺼내면서 찾아야한다.
'CS > 자료구조' 카테고리의 다른 글
| 이진 트리(Binary Tree) 개념 및 구현 (0) | 2022.06.17 |
|---|---|
| 트리(Tree) 개념 및 구현 (0) | 2022.06.16 |
| 큐(Queue) 개념 및 구현 (0) | 2022.06.03 |
| 더블 링크드리스트(Doubly Linked List) 개념과 구현 (0) | 2022.05.20 |
| 링크드리스트(LinkedList) 개념 및 구현 (0) | 2022.05.20 |
스택이란
스택은 뭔가를 아래에서부터 위로 쌓아 얹어 올리도록 하는 자료구조이다.
스택은 오직 top에서 삭제, 추가가 이루어지기 때문에 중간 인덱스에 데이터 변경을 할 수 없다. 특정위치의 데이터를 추가/삭제 하고싶다면 해당 위치까지 pop을 해야한다.
따라서 스택은 가장 마지막에 들어간 데이터가 제일 먼저 나오고(Last In - First Out) 가장 먼저 들어간 데이터는 가장 나중에 나오게(First In - Last Out)된다.
스택의 주요 기능
- 삽입
- 제거
스택의 대표적인 기능은 위와 같이 2가지 연산이 있다. 먼저 삽입은 스택 위에 새로운 요소를 쌓는 작업이다.
제거는 스택에서 최상위 요소를 걷어내는 작업이다.


스택 구현 방식
스택을 구현하는 방식으로는 아래와 같이 2가지가 있다
- 배열을 이용
- 링크드리스트를 이용
배열방식은 구현방식이 간단하지만 동적으로 스택 용량 조절이 어렵다는 단점이 있다.
링크드리스트는 구현방식이 배열에 비해 까다롭지만 스택 용량 조절이 동적으로 가능하다는 장점이 존재한다.
배열로 구현하는 스택
배열 기반의 스택은 스택 생성 초기 사용자가 부여한 크기만큼의 데이터 공간을 한꺼번에 생성한다. 그리고 최상위 노드의 위치를 나타내는 변수(Top)를 이용하여 삽입과 제거 연산을 수행한다.
스택이 가지고 있어야할 기본 변수는 최상위 노드의 위치(Top), 배열, 배열의 크기이다.
int capacity;
int top;
Object[] data;스택의 생성
public ArrayStack(int capacity)
{
this.capacity = capacity;
this.top = 0;
this.data = new Object[capacity];
}생성자를 통해 배열의 크기를 capacity에 저장하고 최상위 노드의 위치를 가리킬 Top은 0으로 초기화한다.
Top은 노드가 쌓일 때마다 +1, 삭제될 때마다 -1이 된다.
삽입연산
void push(T data)
{
this.data[top++] = data;
}데이터가 삽입되면 최상위 노드위치(Top)에 데이터를 넣은 후 Top을 증가시킨다.
제거연산
Object pop()
{
data[top] = null;
return data[--top];
}삭제시에는 Top을 감소시킨후 헤당 배열 값을 반환하면 됩니다. 이때 Top이 갖고 있는 값은 실제 최상위 노드가 배열 내에서 위치하는 인덱스 값보다 1만큼 크다는것이다.
크기계산
int getSize()
{
return top;
}스택의 크기는 top을 반환하면 된다. top은 스택의 노드가 추가될때마다 +1이 되기 때문에 이는 크기를 뜻하기도 한다.
빈값체크
boolean isEmpty()
{
return (top == 0);
}top이 0이란 것은 스택에 아무것도 없다는 의미이기 때문에 true를 반환하면 된다.
링크드 리스트로 구현하는 스택
링크드리스트로 구현을 하면 스택의 용량에 제한을 두지 않아도 된다. 그리고 노드는 자신의 위에 위치하는 노드에 대한 포인터를 갖고 있어야 한다. 노드의 구조는 아래와 같다.
class Node
{
private T data;
private Node nextNode;
public Node(T data) {
this.data = data;
this.nextNode = null;
}
public T getData() {
return data;
}
}링크드리스트 스택은 배열기반 스택과는 달리 스택의 용량, 최상위 노드의 인덱스가 없다. 대신 링크드리스트의 헤드(List)와 테일(Top)이 존재한다.
Node List;
Node Top;List는 스택이 기반하고 있는 링크드 리스트에 접근할 수 있게 하고 Top 포인터는 링크드 리스트의 테일을 가리킴으로써 최상위 노드에 대한 정보를 유지한다.
스택의 생성
스택생성 시에는 List, Top 만 생성하기때문에 기본 생성자를 사용한다.
스택에 노드를 삽입할때 노드는 data만 설정하고 nextnode는 null 인 상태로 나둔다.
Node newNode = new Node(newData);삽입연산
이 연산은 링크드리스트의 추가 연산과 비슷하다. 먼저 최상위 노드(Top)을 찾은 다음, 여기에 새 노드를 얹기만 하면 된다. 그런다음 Top은 새 노드를 가리키게 한다.
void push(T newData)
{
Node newNode = new Node(newData);
if(List == null)
{
List = newNode;
}
else
{
Node oldTop = List;
while(oldTop.nextNode != null)
{
oldTop = oldTop.nextNode;
}
oldTop.nextNode = newNode;
}
Top = newNode;
}삽입할때 스택이 빈 경우와 비지않은 경우를 고려해야한다.
제거연산
제거는 아래와 같이 수행된다
- 현재 최상위 노드(Top)를 다른 변수에 복사해둔다
- 현재 최상위 노드의 바로 이전 노드를 찾는다.
- Top을 찾은 이전 노드로 바꾼다.
- 복사해준 옛 최상위 노드를 반환한다.
Node pop()
{
Node TopNode = Top;
if (List == Top)
{
List = null;
Top = null;
}
else
{
Node currentTop = List;
while(currentTop != null && currentTop.nextNode != Top)
{
currentTop = currentTop.nextNode;
}
Top = currentTop;
currentTop.nextNode = null;
}
return TopNode;
}크기계산
링크드리스트의 크기계산과 동일하며 헤드부터 순회하며 count 한다.
int getSize()
{
int count = 0;
Node current = List;
while(current != null)
{
current = current.nextNode;
count++;
}
return count;
}빈값체크
헤드(List) 값이 null라면 데이터가 없는 것이기 때문에 null일때 true를 반환한다.
boolean isEmpty()
{
return (List == null);
}요약
이렇게 구현해봄으로써 알 수 있는 장단점으로는
장점
- top 을 통해 접근하기 때문에 데이터 삽입, 삭제가 빠르다
단점
- top 위치 이외의 데이터에 접근하려면 모든 데이터를 꺼내면서 찾아야한다.
'CS > 자료구조' 카테고리의 다른 글
| 이진 트리(Binary Tree) 개념 및 구현 (0) | 2022.06.17 |
|---|---|
| 트리(Tree) 개념 및 구현 (0) | 2022.06.16 |
| 큐(Queue) 개념 및 구현 (0) | 2022.06.03 |
| 더블 링크드리스트(Doubly Linked List) 개념과 구현 (0) | 2022.05.20 |
| 링크드리스트(LinkedList) 개념 및 구현 (0) | 2022.05.20 |
