2022.06.16 - [자료구조] - 트리(Tree) 개념 및 구현
트리(Tree) 개념 및 구현
트리는 말 그대로 나무와 유사한 자료구조를 말한다. 이는 사회나 컴퓨터공학에서 흔히 사용되고 있다. 예를 들어보자면 회사 조직도가 있다. 회사의 사장이 나무의 뿌리에 해당한다고 하면, 사
rooftoproom-whale.tistory.com
우리는 앞서 트리에 대한 기본적인 내용에 대해 알아봤다. LCRS 트리는 N개의 자식을 가지는 트리였는데 지금 알아볼 이진 트리는 자식을 최대 2개까지 가질 수 있는 트리이다. 그래서 이름도 이진(Binary) 이다.
자식이 많으면 좋은게 아닌가? 왜 2명으로 제한을 둘까? 라는 의문이 생기는데 이 이진트리를 통해 탐색과 수식 처리하는 알고리즘이 존재하기때문에 이진 트리는 매우 중요하다.
이진 트리의 여러 형태
이진 트리의 제일 중요한 특징은 노드의 최대 차수가 2라는 것이다. 즉 특정 노드의 자식노드가 아예 없거나 하나 또는 둘 뿐이라는 것이다.
포화 이진 트리(Full Binary Tree)
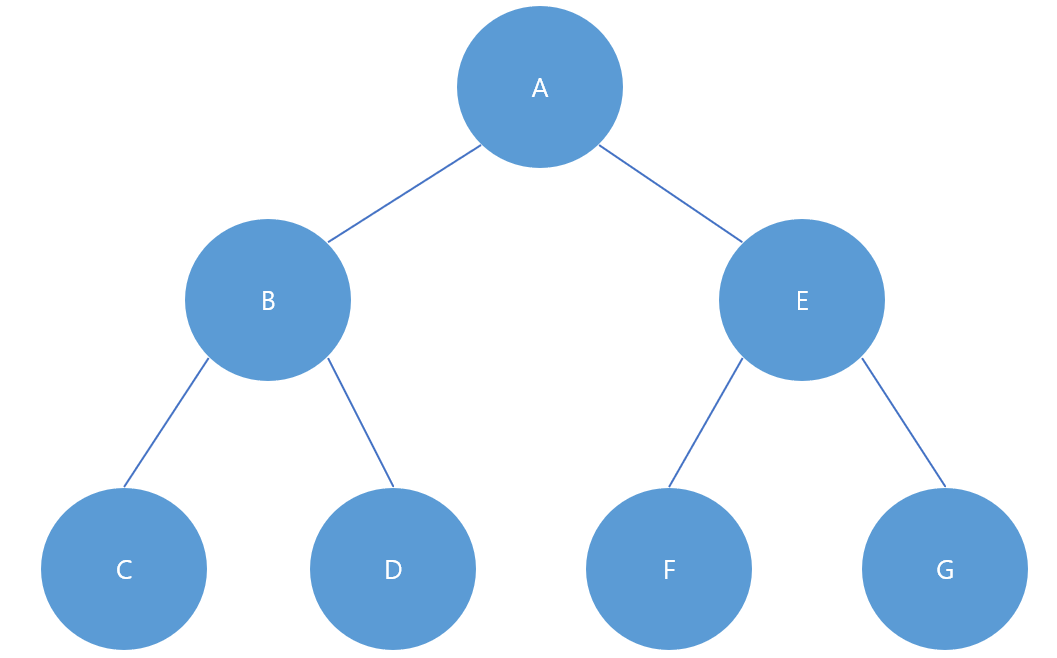
위와 같은 그림을 포화 이진 트리라고 한다. 잎(Leaf) 노드 들이 모두 같은 깊이에 존재하고 잎(Leaf) 노드를 제외한 모든 노드가 대대손손 자식을 둘씩 가지고 있는 것이 특징이다.
완전 이진 트리(Complete Binary Tree)
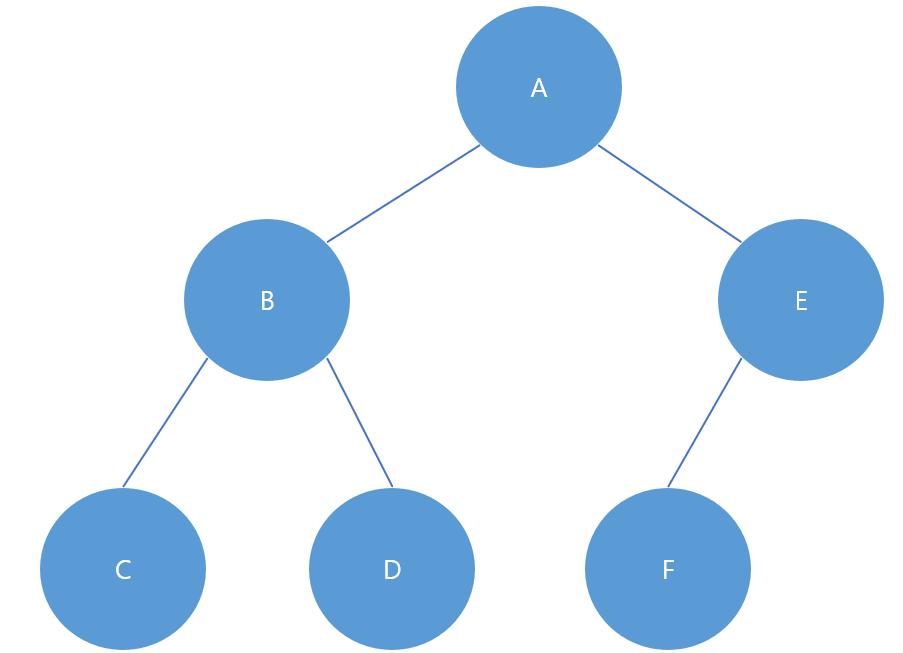
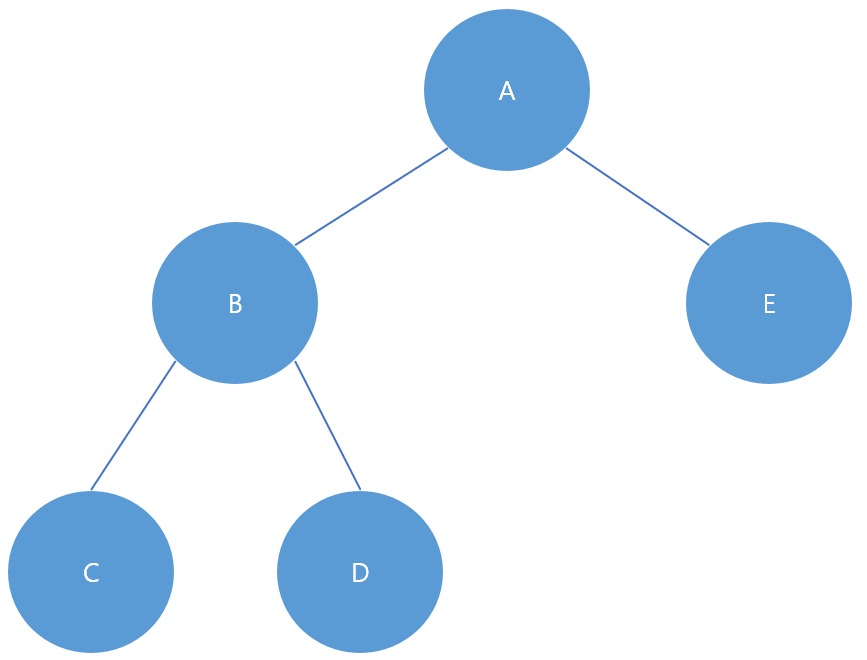
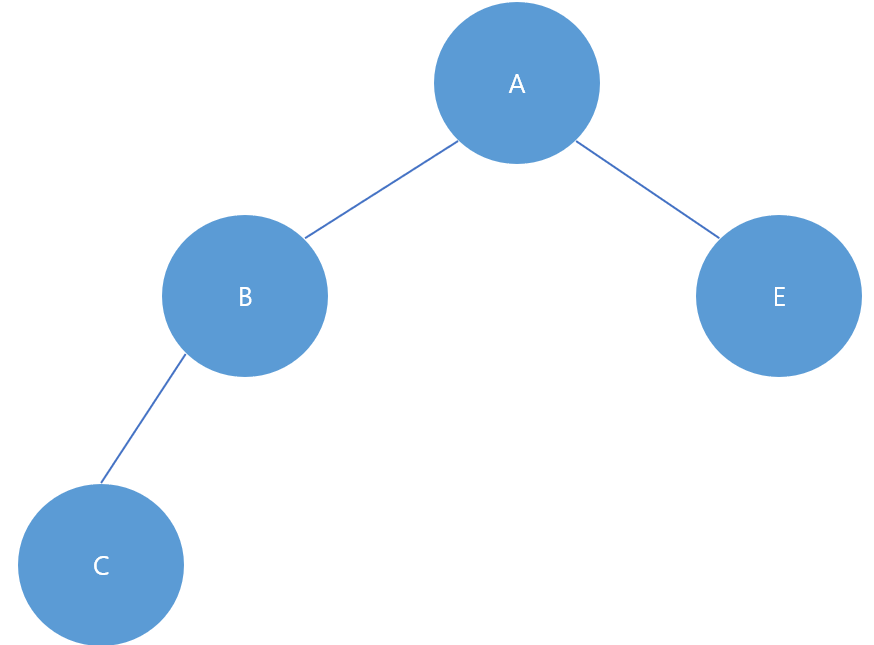
그림처럼 포화 이진 트리를 이루기 전 단계의 트리를 완전 이진 트리라고 부른다. 잎(Leaf) 노드 들이 모두 같은 깊이에 있지 않고 잎 노드를 제외한 노드의 자식이 하나라도 둘이 아닌것이 특징이다.
왜 이렇게 이진 트리안에서도 여러 종류가 존재할까? 그건 이진 트리는 일반 트리처럼 나무 모양의 자료를 담기 위한 자료 구조가 아니라 컴파일러나 검색 등에 사용되는 특수 자료구조이다.
특히 이진 트리를 이용한 검색에서는 높은 성능을 위해 트리의 노드들을 가능한 한 완전한 모습으로 배치하는 것이 필수이다. 그래서 이러한 종류를 알고 있어야 한다.
높이 균형 트리(Height Balanced Tree), 완전 높이 균형 트리(Completely Height Balanced Tree)
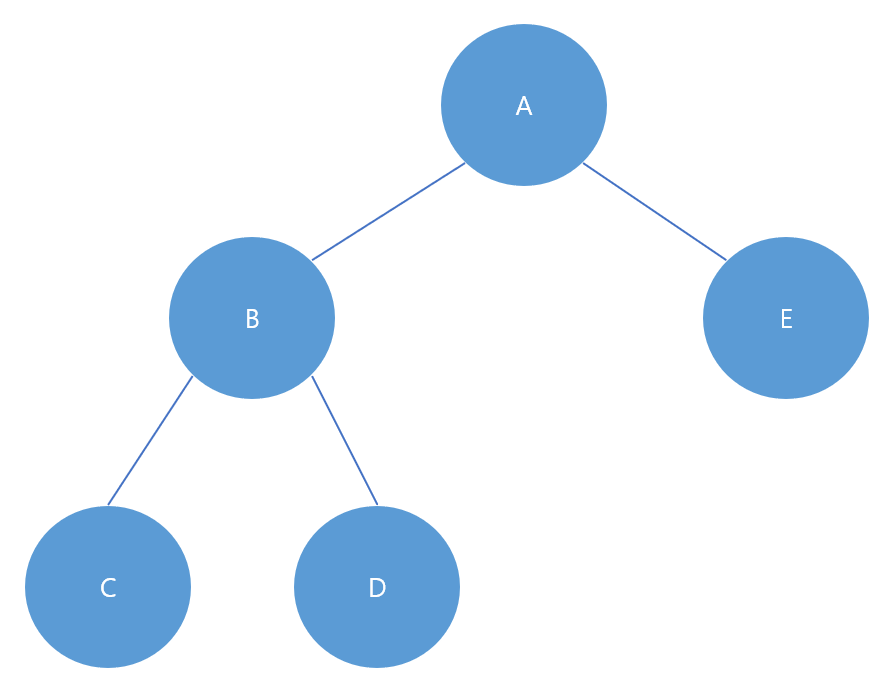
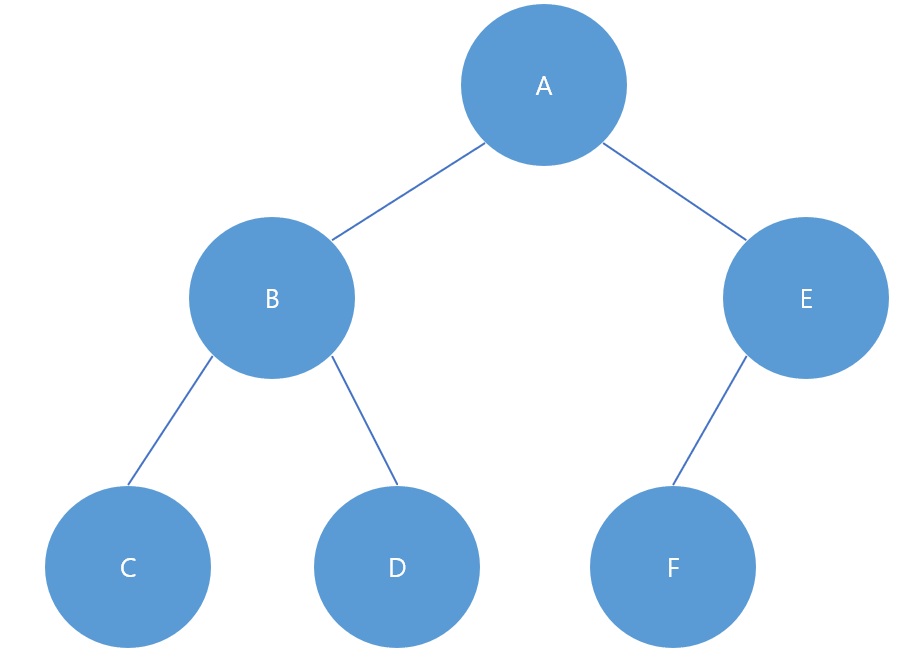
위 그림과 같이 루트 노드 기준으로 왼쪽 하위 트리와 오른쪽 하위 트리의 높이가 1이상 차이나지 않는 이진 트리를 말한다. 그렇다면 완전 높이 균형 트리가 존재하는데 이는 왼쪽 하위 트리와 오른쪽 하위 트리의 높이가 같은 트리를 말하는 것이다.
이진 트리의 순회
순회는 간단히 말해 트리 내의 노드들 사이를 돌아다니는 것을 말한다. 몇 가지 규칙에 근거해서 이진 트리 내부를 돌아다니며 효율적인 방법으로 원하는 데이터를 접근한다.
순회의 종류는 아래와 같다.
- 전위 순회(Preorder Traversal) : 루트 노드부터 잎 노드까지 아래 방향으로 방문
- 중위 순회(Inorder Traversal) : 왼쪽 하위 트리부터 오른쪽 하위 트리 방향으로 방문
- 후위 순회(Postorder Traversal) : 루트, 왼쪽 하위 트리, 오른쪽 하위 트리 순으로 방문
전위 순회
- 루트 노드부터 시작해서 아래로 내려오면서
- 왼쪽 하위 트리를 방문하고 왼쪽 하위 트리의 방문이 끝나면
- 오른쪽 하위 트리를 방문
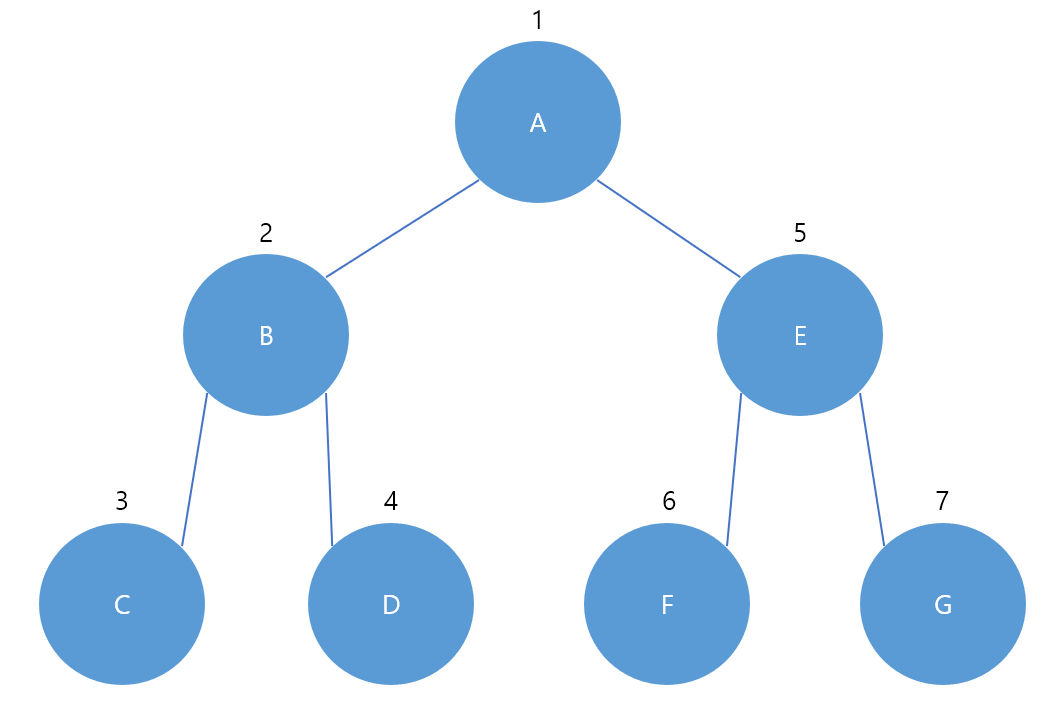
예를 들어 일단 위의 그림에서 루트, 왼쪽 하위, 오른쪽 하위 총 3 부분으로 나눈다.
루트를 순회 후 왼쪽 하위 트리로 이동한다.(A)
왼쪽 하위 트리를 전체로 보자면 B가 루트이고 C가 왼쪽 하위 트리이기 때문에 C까지 순회한다. (A->B->C)
더이상 왼쪽 하위 트리가 없기 때문에 오른쪽 하위 트리인 D로 진행한다(A->B->C->D)
즉, 루트 -> 왼쪽 하위 -> 왼쪽 하위 순회가 다 끝난다면 오른쪽 하위 순회 의 순서로 진행을 하면 아래와 같은 결과가 나온다.
( A ( B ( C D ) ) ( E ( F G ) ) )
중위 순회
- 왼쪽 하위 트리부터 시작해서
- 루트를 거쳐
- 오른쪽 하위 트리를 방문
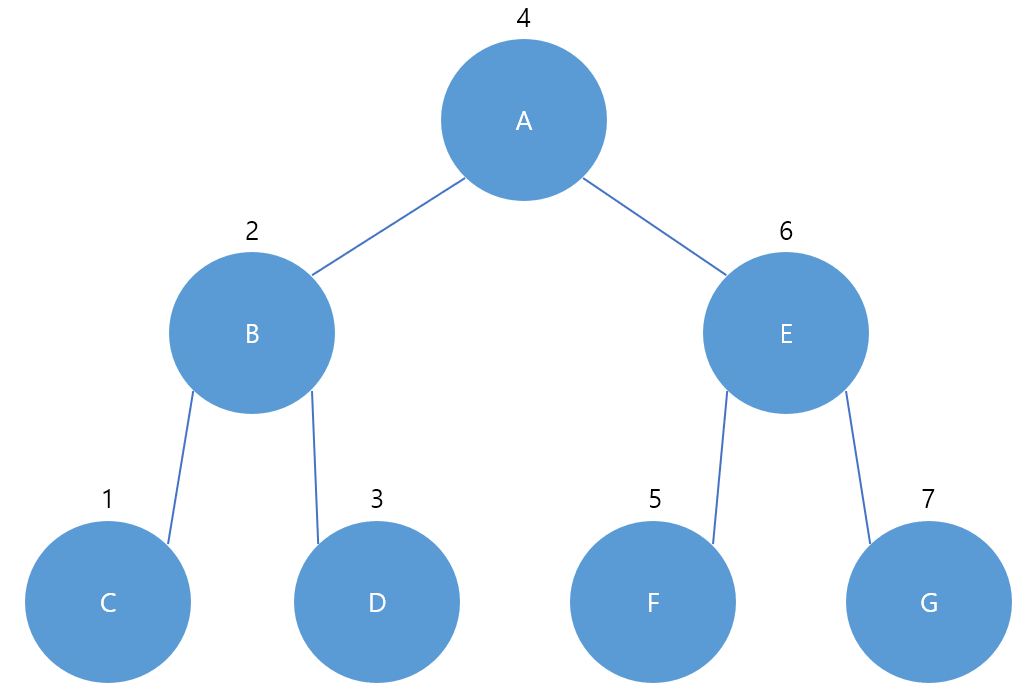
왼쪽 하위 트리에서 시작한다는 말은 트리에서의 가장 왼쪽의 잎 노드부터 시작한다는 뜻이고 이 잎 노드에서부터 시작된 순회는 부모 노드를 방문한 후 자신의 형제 노드를 방문한다. 이렇게 최소 단위의 하위 트리 순회가 끝나면 그 윗 단계 하위 트리에 대해 순회를 계속한다.
이 중위 순회가 응용되는 대표적인 사례는 수식 트리(Expression Tree)이다.
후위 순회
- 왼쪽 하위 트리부터 시작해서
- 오른쪽 하위 트리를 방문하고 오른쪽 하위트리 방문이 끝나면
- 루트 방문
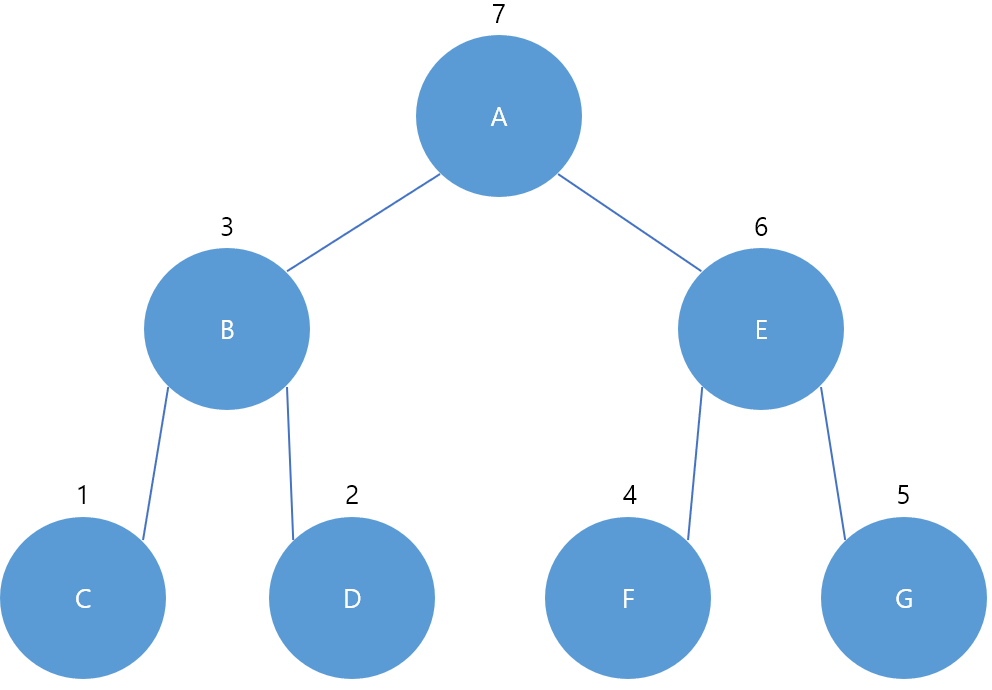
방문 순서는 왼쪽 하위 트리, 오른쪽 하위 트리, 루트 노드 순이다. 이 순서는 하위 트리의 하위 트리, 또 그 하위 트리의 하위 트리에 대해 똑같이 적용된다. 하위 트리가 잎 노드라면 중단된다.
이 순회 방식은 후위 표기식에서 사용된다.
이진 트리 구현하기
이진트리의 주요 연산은 아래와 같다.
- 노드 선언 및 생성
- 전위 순회를 응용한 이진 트리 출력
- 중위 순회를 응용한 이진 트리 출력
- 후위 순회를 응용한 이진 트리 출력
- 후위 순회를 응용한 이진 트리 소멸
노드 선언 및 생성
public class SBTNode<T>
{
private SBTNode<T> Left;
private SBTNode<T> Right;
private final T data;
public SBTNode(T data)
{
this.data = data;
}
public T getData() {
return data;
}
public SBTNode<T> getLeft() {
return Left;
}
public void setLeft(SBTNode<T> left) {
Left = left;
}
public SBTNode<T> getRight() {
return Right;
}
public void setRight(SBTNode<T> right) {
Right = right;
}
}이진 트리 노드의 기본 구조는 왼쪽 자식을 가리키는 Left, 오른쪽 자식을 가리키는 Right, 데이터를 담는 data필드로 구성된다. 노드 생성 시에는 left, right가 null이고 data는 입력받는 생성자를 사용한다.
전위 순회를 응용한 이진 트리 출력 구현
public void preOrderPrintTree(SBTNode<T> node)
{
if (node == null) return;
System.out.print(" " + node.getData());
preOrderPrintTree(node.getLeft());
preOrderPrintTree(node.getRight());
}매개 변수로 루트인 노드를 입력 받으면 루트 출력 후 왼쪽 하위 트리 , 오른쪽 하위 트리 순으로 순회를 진행한다.
이 순서가 재귀 형태로 계속 진행되기 때문에 재귀 호출을 사용한다.
중위 순회를 응용한 이진 트리 출력 구현
public void inOrderPrintTree(SBTNode<T> node)
{
if (node == null) return;
inOrderPrintTree(node.getLeft());
System.out.print(" " + node.getData());
inOrderPrintTree(node.getRight());
}매개 변수로 루트인 노드를 입력 받고 왼쪽 하위 트리, 루트, 오른쪽 하위 트리 순으로 방문한다.
후위 순회를 응용한 이진 트리 출력 구현
public void postOrderPrintTree(SBTNode<T> node)
{
if (node == null) return;
postOrderPrintTree(node.getLeft());
postOrderPrintTree(node.getRight());
System.out.print(" " + node.getData());
}매개 변수로 루트인 노드를 입력 받고 왼쪽 하위 트리, 오른쪽 하위 트리, 루트 순으로 방문한다.
후위 순회를 응용하여 트리 소멸 함수 구현
public void destroyTree(SBTNode<T> node)
{
if(node == null) return;
destroyTree(node.getLeft());
destroyTree(node.getRight());
node = null;
}트리를 구축할 때는 노드들이 어떤 순으로 생성되든 상관없지만 트리를 제거할 때는 반드시 잎 노드부터 제거해야한다.
따라서 잎 노드부터 방문하여 루트 노드까지 거슬러 올라가며 방문하는 후위 순회를 이용하면 이진 트리 전체를 문제없이 제거할 수 있다.
예제소스
public class BinaryTreeTest
{
public static void main(String[] args) {
SBTNode<Character> A = new SBTNode<>('A');
SBTNode<Character> B = new SBTNode<>('B');
SBTNode<Character> C = new SBTNode<>('C');
SBTNode<Character> D = new SBTNode<>('D');
SBTNode<Character> F = new SBTNode<>('F');
SBTNode<Character> E = new SBTNode<>('E');
SBTNode<Character> G = new SBTNode<>('G');
A.setLeft(B);
B.setLeft(C);
B.setRight(D);
A.setRight(E);
E.setLeft(F);
E.setRight(G);
BinaryTree<Character> binaryTree = new BinaryTree<>();
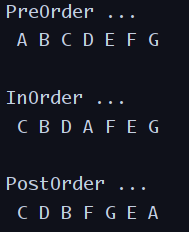
System.out.println("PreOrder ...");
binaryTree.preOrderPrintTree(A);
System.out.println();
System.out.println();
System.out.println("InOrder ...");
binaryTree.inOrderPrintTree(A);
System.out.println();
System.out.println();
System.out.println("PostOrder ...");
binaryTree.postOrderPrintTree(A);
System.out.println();
System.out.println();
}
}
'CS > 자료구조' 카테고리의 다른 글
| 트리(Tree) 개념 및 구현 (0) | 2022.06.16 |
|---|---|
| 큐(Queue) 개념 및 구현 (0) | 2022.06.03 |
| 스택(Stack) 개념 및 구현 (0) | 2022.05.25 |
| 더블 링크드리스트(Doubly Linked List) 개념과 구현 (0) | 2022.05.20 |
| 링크드리스트(LinkedList) 개념 및 구현 (0) | 2022.05.20 |
2022.06.16 - [자료구조] - 트리(Tree) 개념 및 구현
트리(Tree) 개념 및 구현
트리는 말 그대로 나무와 유사한 자료구조를 말한다. 이는 사회나 컴퓨터공학에서 흔히 사용되고 있다. 예를 들어보자면 회사 조직도가 있다. 회사의 사장이 나무의 뿌리에 해당한다고 하면, 사
rooftoproom-whale.tistory.com
우리는 앞서 트리에 대한 기본적인 내용에 대해 알아봤다. LCRS 트리는 N개의 자식을 가지는 트리였는데 지금 알아볼 이진 트리는 자식을 최대 2개까지 가질 수 있는 트리이다. 그래서 이름도 이진(Binary) 이다.
자식이 많으면 좋은게 아닌가? 왜 2명으로 제한을 둘까? 라는 의문이 생기는데 이 이진트리를 통해 탐색과 수식 처리하는 알고리즘이 존재하기때문에 이진 트리는 매우 중요하다.
이진 트리의 여러 형태
이진 트리의 제일 중요한 특징은 노드의 최대 차수가 2라는 것이다. 즉 특정 노드의 자식노드가 아예 없거나 하나 또는 둘 뿐이라는 것이다.
포화 이진 트리(Full Binary Tree)

위와 같은 그림을 포화 이진 트리라고 한다. 잎(Leaf) 노드 들이 모두 같은 깊이에 존재하고 잎(Leaf) 노드를 제외한 모든 노드가 대대손손 자식을 둘씩 가지고 있는 것이 특징이다.
완전 이진 트리(Complete Binary Tree)



그림처럼 포화 이진 트리를 이루기 전 단계의 트리를 완전 이진 트리라고 부른다. 잎(Leaf) 노드 들이 모두 같은 깊이에 있지 않고 잎 노드를 제외한 노드의 자식이 하나라도 둘이 아닌것이 특징이다.
왜 이렇게 이진 트리안에서도 여러 종류가 존재할까? 그건 이진 트리는 일반 트리처럼 나무 모양의 자료를 담기 위한 자료 구조가 아니라 컴파일러나 검색 등에 사용되는 특수 자료구조이다.
특히 이진 트리를 이용한 검색에서는 높은 성능을 위해 트리의 노드들을 가능한 한 완전한 모습으로 배치하는 것이 필수이다. 그래서 이러한 종류를 알고 있어야 한다.
높이 균형 트리(Height Balanced Tree), 완전 높이 균형 트리(Completely Height Balanced Tree)


위 그림과 같이 루트 노드 기준으로 왼쪽 하위 트리와 오른쪽 하위 트리의 높이가 1이상 차이나지 않는 이진 트리를 말한다. 그렇다면 완전 높이 균형 트리가 존재하는데 이는 왼쪽 하위 트리와 오른쪽 하위 트리의 높이가 같은 트리를 말하는 것이다.
이진 트리의 순회
순회는 간단히 말해 트리 내의 노드들 사이를 돌아다니는 것을 말한다. 몇 가지 규칙에 근거해서 이진 트리 내부를 돌아다니며 효율적인 방법으로 원하는 데이터를 접근한다.
순회의 종류는 아래와 같다.
- 전위 순회(Preorder Traversal) : 루트 노드부터 잎 노드까지 아래 방향으로 방문
- 중위 순회(Inorder Traversal) : 왼쪽 하위 트리부터 오른쪽 하위 트리 방향으로 방문
- 후위 순회(Postorder Traversal) : 루트, 왼쪽 하위 트리, 오른쪽 하위 트리 순으로 방문
전위 순회
- 루트 노드부터 시작해서 아래로 내려오면서
- 왼쪽 하위 트리를 방문하고 왼쪽 하위 트리의 방문이 끝나면
- 오른쪽 하위 트리를 방문

예를 들어 일단 위의 그림에서 루트, 왼쪽 하위, 오른쪽 하위 총 3 부분으로 나눈다.
루트를 순회 후 왼쪽 하위 트리로 이동한다.(A)
왼쪽 하위 트리를 전체로 보자면 B가 루트이고 C가 왼쪽 하위 트리이기 때문에 C까지 순회한다. (A->B->C)
더이상 왼쪽 하위 트리가 없기 때문에 오른쪽 하위 트리인 D로 진행한다(A->B->C->D)
즉, 루트 -> 왼쪽 하위 -> 왼쪽 하위 순회가 다 끝난다면 오른쪽 하위 순회 의 순서로 진행을 하면 아래와 같은 결과가 나온다.
( A ( B ( C D ) ) ( E ( F G ) ) )
중위 순회
- 왼쪽 하위 트리부터 시작해서
- 루트를 거쳐
- 오른쪽 하위 트리를 방문

왼쪽 하위 트리에서 시작한다는 말은 트리에서의 가장 왼쪽의 잎 노드부터 시작한다는 뜻이고 이 잎 노드에서부터 시작된 순회는 부모 노드를 방문한 후 자신의 형제 노드를 방문한다. 이렇게 최소 단위의 하위 트리 순회가 끝나면 그 윗 단계 하위 트리에 대해 순회를 계속한다.
이 중위 순회가 응용되는 대표적인 사례는 수식 트리(Expression Tree)이다.
후위 순회
- 왼쪽 하위 트리부터 시작해서
- 오른쪽 하위 트리를 방문하고 오른쪽 하위트리 방문이 끝나면
- 루트 방문

방문 순서는 왼쪽 하위 트리, 오른쪽 하위 트리, 루트 노드 순이다. 이 순서는 하위 트리의 하위 트리, 또 그 하위 트리의 하위 트리에 대해 똑같이 적용된다. 하위 트리가 잎 노드라면 중단된다.
이 순회 방식은 후위 표기식에서 사용된다.
이진 트리 구현하기
이진트리의 주요 연산은 아래와 같다.
- 노드 선언 및 생성
- 전위 순회를 응용한 이진 트리 출력
- 중위 순회를 응용한 이진 트리 출력
- 후위 순회를 응용한 이진 트리 출력
- 후위 순회를 응용한 이진 트리 소멸
노드 선언 및 생성
public class SBTNode<T>
{
private SBTNode<T> Left;
private SBTNode<T> Right;
private final T data;
public SBTNode(T data)
{
this.data = data;
}
public T getData() {
return data;
}
public SBTNode<T> getLeft() {
return Left;
}
public void setLeft(SBTNode<T> left) {
Left = left;
}
public SBTNode<T> getRight() {
return Right;
}
public void setRight(SBTNode<T> right) {
Right = right;
}
}이진 트리 노드의 기본 구조는 왼쪽 자식을 가리키는 Left, 오른쪽 자식을 가리키는 Right, 데이터를 담는 data필드로 구성된다. 노드 생성 시에는 left, right가 null이고 data는 입력받는 생성자를 사용한다.
전위 순회를 응용한 이진 트리 출력 구현
public void preOrderPrintTree(SBTNode<T> node)
{
if (node == null) return;
System.out.print(" " + node.getData());
preOrderPrintTree(node.getLeft());
preOrderPrintTree(node.getRight());
}매개 변수로 루트인 노드를 입력 받으면 루트 출력 후 왼쪽 하위 트리 , 오른쪽 하위 트리 순으로 순회를 진행한다.
이 순서가 재귀 형태로 계속 진행되기 때문에 재귀 호출을 사용한다.
중위 순회를 응용한 이진 트리 출력 구현
public void inOrderPrintTree(SBTNode<T> node)
{
if (node == null) return;
inOrderPrintTree(node.getLeft());
System.out.print(" " + node.getData());
inOrderPrintTree(node.getRight());
}매개 변수로 루트인 노드를 입력 받고 왼쪽 하위 트리, 루트, 오른쪽 하위 트리 순으로 방문한다.
후위 순회를 응용한 이진 트리 출력 구현
public void postOrderPrintTree(SBTNode<T> node)
{
if (node == null) return;
postOrderPrintTree(node.getLeft());
postOrderPrintTree(node.getRight());
System.out.print(" " + node.getData());
}매개 변수로 루트인 노드를 입력 받고 왼쪽 하위 트리, 오른쪽 하위 트리, 루트 순으로 방문한다.
후위 순회를 응용하여 트리 소멸 함수 구현
public void destroyTree(SBTNode<T> node)
{
if(node == null) return;
destroyTree(node.getLeft());
destroyTree(node.getRight());
node = null;
}트리를 구축할 때는 노드들이 어떤 순으로 생성되든 상관없지만 트리를 제거할 때는 반드시 잎 노드부터 제거해야한다.
따라서 잎 노드부터 방문하여 루트 노드까지 거슬러 올라가며 방문하는 후위 순회를 이용하면 이진 트리 전체를 문제없이 제거할 수 있다.
예제소스
public class BinaryTreeTest
{
public static void main(String[] args) {
SBTNode<Character> A = new SBTNode<>('A');
SBTNode<Character> B = new SBTNode<>('B');
SBTNode<Character> C = new SBTNode<>('C');
SBTNode<Character> D = new SBTNode<>('D');
SBTNode<Character> F = new SBTNode<>('F');
SBTNode<Character> E = new SBTNode<>('E');
SBTNode<Character> G = new SBTNode<>('G');
A.setLeft(B);
B.setLeft(C);
B.setRight(D);
A.setRight(E);
E.setLeft(F);
E.setRight(G);
BinaryTree<Character> binaryTree = new BinaryTree<>();
System.out.println("PreOrder ...");
binaryTree.preOrderPrintTree(A);
System.out.println();
System.out.println();
System.out.println("InOrder ...");
binaryTree.inOrderPrintTree(A);
System.out.println();
System.out.println();
System.out.println("PostOrder ...");
binaryTree.postOrderPrintTree(A);
System.out.println();
System.out.println();
}
}
'CS > 자료구조' 카테고리의 다른 글
| 트리(Tree) 개념 및 구현 (0) | 2022.06.16 |
|---|---|
| 큐(Queue) 개념 및 구현 (0) | 2022.06.03 |
| 스택(Stack) 개념 및 구현 (0) | 2022.05.25 |
| 더블 링크드리스트(Doubly Linked List) 개념과 구현 (0) | 2022.05.20 |
| 링크드리스트(LinkedList) 개념 및 구현 (0) | 2022.05.20 |
