트리는 말 그대로 나무와 유사한 자료구조를 말한다. 이는 사회나 컴퓨터공학에서 흔히 사용되고 있다.
예를 들어보자면 회사 조직도가 있다. 회사의 사장이 나무의 뿌리에 해당한다고 하면, 사장 밑에 있는 각 부서의 부장들은 뿌리에서 뻗어 나온 가지라고 할 수 있다. 부장 밑에 있는 차장, 과장, 대리 등은 부장이라는 가지에서 뻗어 나온 잔 가지가 된다.
컴퓨터 공학에서도 활용도가 높은 자료구조인데 우선 운영체제의 파일 시스템이 트리 구조로 이루어져 있고, HTML이나 XML 문서를 다룰 때 사용하는 DOM(Document Object Model)도 트리 구조이다. 이뿐만 아니라 검색 엔진이나 데이터베이스도 트리 자료구조에 기반해서 구현된다.
트리의 구성 요소
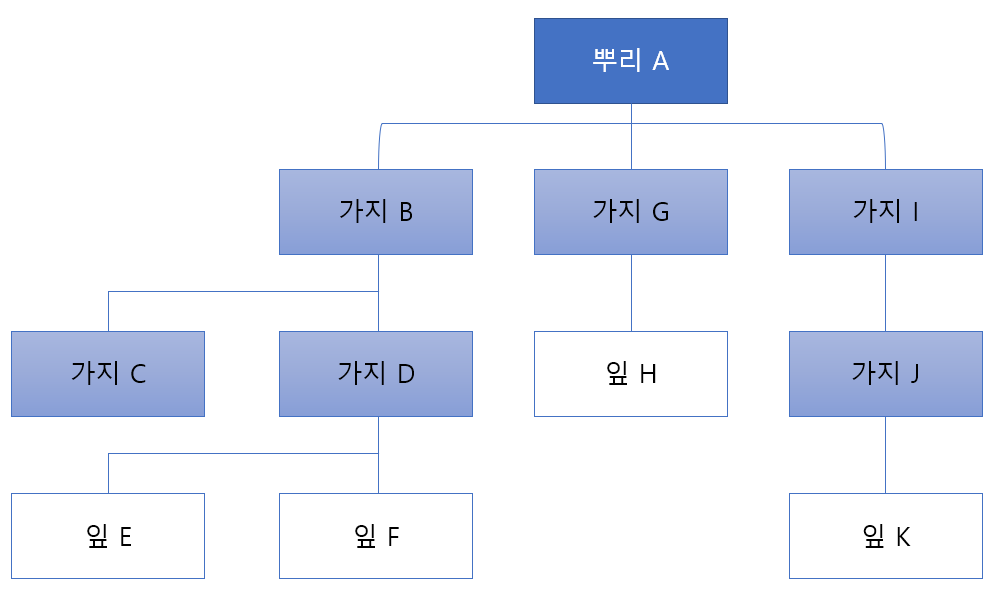
트리는 그림과 같이 뿌리(Root), 가지(Branch), 잎(Leaf) 세가지 요소로 이루어져 있다.
뿌리, 가지, 잎 모두 실제로는 똑같은 노드이다. 이들은 트리 내의 위치에 때라 명칭만 달라질 뿐이다.
뿌리인 루트는 트리 자료구조의 가장 위에 있는 노드를 가리키고
가지는 루트와 잎 사이에 있는 모든 노드
잎은 가지의 끝에 매달려 있는 노드를 말한다.
이외에 트리 관련 용어들이 존재하는데 한번 알아보겠다.
- 부모(Parent) : 특정 노드 위에 있는 노드를 부모라 부른다 (ex: B는 C, D의 부모)
- 자식(Children) : 특정 노드 밑에 있는 노드를 자식이라 부른다(ex: C,D는 B의 자식)
- 형제(Sibling) : 한 부모 밑에서 태어난 노드를 형제라고 한다.(ex: C,D는 형제)
- 깊이(Depth) : 루트 노드에서 해당 노드까지의 경로의 길이(ex:G는 깊이가 1인 노드)
- 레벨(Level) : 깊이가 같은 노드 집합(ex: 레벨 2인 노드는 C, D, H, J)
- 높이(Height) : 가장 깊은 곳에 있는 잎 노드까지의 깊이(ex: 가장 깊은 곳은 E, F, K 이므로 높이는 3)
- 차수(Degree) : 특정 노드의 자식 노드 개수, 이때 트리의 차수는 트리 내의 있는 노드들 가운데 자식 노드가 가장 많은 노드의 차수를 말한다.(ex: 트리의 차수 : 3, A의 차수 : 3)
노드로 표현하기
트리를 표현하기 위해서 데이터를 담을 노드를 한번 표현해보겠다.
트리 노드를 표현하는 방법에는 2 가지가 있다.
- N-링크 표현법
- 왼쪽 자식-오른쪽 형재 표현법
N-링크 표현법
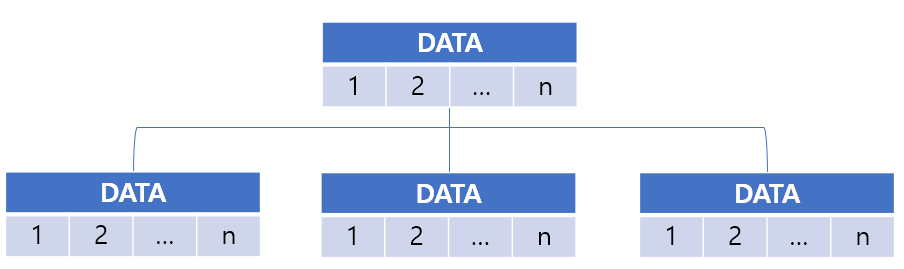
N-링크는 노드의 차수가 N이라면 노드가 N개의 링크를 가지고 있어서 이 링크들이 각각 자식 노드를 가리키도록 노드를 구성하는 방법이다.
허나 차수가 노드마다 달라지는 트리에는 적용하기 어려운 점이 존재한다.
예를 들어 폴더 트리 같은 경우 폴더의 차수가 0일 수도 있고 N개일 수도 있다. 즉 쓰이지 않고 공간만 낭비하는 노드가 존재할 수 있다. 고정적인 데이터 크기를 갖는 방법이라는 것이다.
그래서 나온 방법이 왼쪽 자식-오른쪽 형제 표현법이다
왼쪽 자식-오른쪽 형제 표현법
이름과 같이 왼쪽 자식과 오른쪽 형제에 대한 포인터를 갖고 있는 노드의 구조이다. 이 방법을 사용하면 N개의 차수를 가진 노드의 표현이 두 개의 포인터, 왼쪽 자식-오른쪽 형제만으로 가능하게 된다.
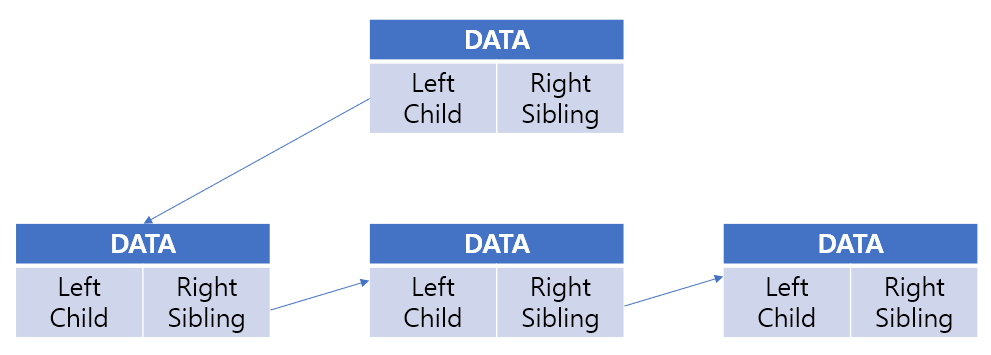
이 표현법을 사용하는 트리에서 어느 한 노드의 모든 자식 노드를 얻으려면 일단 왼쪽 자식 노드에 대한 포인터만 있으면 된다. 이 포인터를 이용해서 왼쪽 자식 노드의 주소를 얻은 후, 이 자식 노드의 오른쪽 형제 노드의 주소를 얻고, 또 그다음 오른쪽 형제 노드의 주소를 계속해서 얻어 나가면 결국 모든 자식 노드를 얻을 수 있다.
트리 구현하기
트리를 구현하는 방식으로는 앞서 설명한 왼쪽 자식-오른쪽 형제(Left Child Right Sibling), LCRS를 사용하겠다.
주요 연산은 아래와 같다
- 노드 선언 및 생성
- 자식 노드 연결
- 트리 출력
노드 선언 및 생성
먼저 노드는 데이터를 담는 Data필드, 왼쪽 자식(Left Child), 오른쪽 자식(Right Sibling)을 가리키는 두 개의 참조값으로 구성된다.
public class LCRSNode<T>
{
private LCRSNode<T> LeftChild;
private LCRSNode<T> RightSibling;
private final T Data;
public LCRSNode(T data) {
Data = data;
}
public T getData() {
return Data;
}
public LCRSNode<T> getLeftChild() {
return LeftChild;
}
public LCRSNode<T> getRightSibling() {
return RightSibling;
}
public void setLeftChild(LCRSNode<T> leftChild) {
LeftChild = leftChild;
}
public void setRightSibling(LCRSNode<T> rightSibling) {
RightSibling = rightSibling;
}
}노드 생성시 데이터를 입력받고 LeftChild와 RightSibling은 자식 노드를 연결하는 연산에서 추가되기 때문에 null이 초기값이 되도록 하였다
자식 노드 연결하기
public void addChildNode(LCRSNode<T> parent, LCRSNode<T> child)
{
if (parent.getLeftChild() == null)
{
parent.setLeftChild(child);
}
else
{
LCRSNode<T> tempNode = parent.getLeftChild();
while (tempNode.getRightSibling() != null) {
tempNode = tempNode.getRightSibling();
}
tempNode.setRightSibling(child);
}
}매개변수로 부모 노드와 이 부모 노드에 연결할 자식 노드를 받는다.
그 후 먼저 부모 노드인 parent에게 자식 노드가 있는지 검사한다. 만약 없다면 자식이 없는 것이기 때문에 LeftChild에 자식으로 추가해준다.
자식 노드가 있다면 새로운 자식의 형제로 추가될 수 있도록 RightSibling에 추가해준다.
트리 출력
public void printTree(LCRSNode<T> node, int depth)
{
for (int i = 0; i < depth; i++)
System.out.print(" ");
System.out.println(node.getData());
if(node.getLeftChild() != null)
printTree(node.getLeftChild(),depth + 1);
if(node.getRightSibling() != null)
printTree(node.getRightSibling(),depth);
}트리 출력방식은 재귀호출을 통해 깊이 우선 탐색을 하여(사실 LeftChild 우선) LeftChilde가 없을 시에는 RightSibling을 탐색 후 출력하도록 한다.
예제소스
public class LCRSTreeTest
{
public static void main(String[] args)
{
LCRSNode<Character> Root = new LCRSNode<>('A');
LCRSNode<Character> B = new LCRSNode<>('B');
LCRSNode<Character> C = new LCRSNode<>('C');
LCRSNode<Character> D = new LCRSNode<>('D');
LCRSNode<Character> E = new LCRSNode<>('E');
LCRSNode<Character> F = new LCRSNode<>('F');
LCRSNode<Character> G = new LCRSNode<>('G');
LCRSNode<Character> H = new LCRSNode<>('H');
LCRSNode<Character> I = new LCRSNode<>('I');
LCRSNode<Character> J = new LCRSNode<>('J');
LCRSNode<Character> K = new LCRSNode<>('K');
LCRSTree<Character> tree = new LCRSTree<>();
tree.addChildNode(Root,B);
tree.addChildNode(B,C);
tree.addChildNode(B,D);
tree.addChildNode(D,E);
tree.addChildNode(D,F);
tree.addChildNode(Root,G);
tree.addChildNode(G,H);
tree.addChildNode(Root,I);
tree.addChildNode(I,J);
tree.addChildNode(J,K);
tree.printTree(Root, 0);
}
}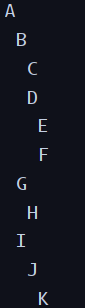
마무리
이렇게 트리의 기본적인 구조와 구현방식을 살펴보았다. 다음에는 현재 많이 쓰이는 이진트리에 대해 알아보겠다.
'CS > 자료구조' 카테고리의 다른 글
| 이진 트리(Binary Tree) 개념 및 구현 (0) | 2022.06.17 |
|---|---|
| 큐(Queue) 개념 및 구현 (0) | 2022.06.03 |
| 스택(Stack) 개념 및 구현 (0) | 2022.05.25 |
| 더블 링크드리스트(Doubly Linked List) 개념과 구현 (0) | 2022.05.20 |
| 링크드리스트(LinkedList) 개념 및 구현 (0) | 2022.05.20 |
트리는 말 그대로 나무와 유사한 자료구조를 말한다. 이는 사회나 컴퓨터공학에서 흔히 사용되고 있다.
예를 들어보자면 회사 조직도가 있다. 회사의 사장이 나무의 뿌리에 해당한다고 하면, 사장 밑에 있는 각 부서의 부장들은 뿌리에서 뻗어 나온 가지라고 할 수 있다. 부장 밑에 있는 차장, 과장, 대리 등은 부장이라는 가지에서 뻗어 나온 잔 가지가 된다.
컴퓨터 공학에서도 활용도가 높은 자료구조인데 우선 운영체제의 파일 시스템이 트리 구조로 이루어져 있고, HTML이나 XML 문서를 다룰 때 사용하는 DOM(Document Object Model)도 트리 구조이다. 이뿐만 아니라 검색 엔진이나 데이터베이스도 트리 자료구조에 기반해서 구현된다.
트리의 구성 요소

트리는 그림과 같이 뿌리(Root), 가지(Branch), 잎(Leaf) 세가지 요소로 이루어져 있다.
뿌리, 가지, 잎 모두 실제로는 똑같은 노드이다. 이들은 트리 내의 위치에 때라 명칭만 달라질 뿐이다.
뿌리인 루트는 트리 자료구조의 가장 위에 있는 노드를 가리키고
가지는 루트와 잎 사이에 있는 모든 노드
잎은 가지의 끝에 매달려 있는 노드를 말한다.
이외에 트리 관련 용어들이 존재하는데 한번 알아보겠다.
- 부모(Parent) : 특정 노드 위에 있는 노드를 부모라 부른다 (ex: B는 C, D의 부모)
- 자식(Children) : 특정 노드 밑에 있는 노드를 자식이라 부른다(ex: C,D는 B의 자식)
- 형제(Sibling) : 한 부모 밑에서 태어난 노드를 형제라고 한다.(ex: C,D는 형제)
- 깊이(Depth) : 루트 노드에서 해당 노드까지의 경로의 길이(ex:G는 깊이가 1인 노드)
- 레벨(Level) : 깊이가 같은 노드 집합(ex: 레벨 2인 노드는 C, D, H, J)
- 높이(Height) : 가장 깊은 곳에 있는 잎 노드까지의 깊이(ex: 가장 깊은 곳은 E, F, K 이므로 높이는 3)
- 차수(Degree) : 특정 노드의 자식 노드 개수, 이때 트리의 차수는 트리 내의 있는 노드들 가운데 자식 노드가 가장 많은 노드의 차수를 말한다.(ex: 트리의 차수 : 3, A의 차수 : 3)
노드로 표현하기
트리를 표현하기 위해서 데이터를 담을 노드를 한번 표현해보겠다.
트리 노드를 표현하는 방법에는 2 가지가 있다.
- N-링크 표현법
- 왼쪽 자식-오른쪽 형재 표현법
N-링크 표현법

N-링크는 노드의 차수가 N이라면 노드가 N개의 링크를 가지고 있어서 이 링크들이 각각 자식 노드를 가리키도록 노드를 구성하는 방법이다.
허나 차수가 노드마다 달라지는 트리에는 적용하기 어려운 점이 존재한다.
예를 들어 폴더 트리 같은 경우 폴더의 차수가 0일 수도 있고 N개일 수도 있다. 즉 쓰이지 않고 공간만 낭비하는 노드가 존재할 수 있다. 고정적인 데이터 크기를 갖는 방법이라는 것이다.
그래서 나온 방법이 왼쪽 자식-오른쪽 형제 표현법이다
왼쪽 자식-오른쪽 형제 표현법
이름과 같이 왼쪽 자식과 오른쪽 형제에 대한 포인터를 갖고 있는 노드의 구조이다. 이 방법을 사용하면 N개의 차수를 가진 노드의 표현이 두 개의 포인터, 왼쪽 자식-오른쪽 형제만으로 가능하게 된다.

이 표현법을 사용하는 트리에서 어느 한 노드의 모든 자식 노드를 얻으려면 일단 왼쪽 자식 노드에 대한 포인터만 있으면 된다. 이 포인터를 이용해서 왼쪽 자식 노드의 주소를 얻은 후, 이 자식 노드의 오른쪽 형제 노드의 주소를 얻고, 또 그다음 오른쪽 형제 노드의 주소를 계속해서 얻어 나가면 결국 모든 자식 노드를 얻을 수 있다.
트리 구현하기
트리를 구현하는 방식으로는 앞서 설명한 왼쪽 자식-오른쪽 형제(Left Child Right Sibling), LCRS를 사용하겠다.
주요 연산은 아래와 같다
- 노드 선언 및 생성
- 자식 노드 연결
- 트리 출력
노드 선언 및 생성
먼저 노드는 데이터를 담는 Data필드, 왼쪽 자식(Left Child), 오른쪽 자식(Right Sibling)을 가리키는 두 개의 참조값으로 구성된다.
public class LCRSNode<T>
{
private LCRSNode<T> LeftChild;
private LCRSNode<T> RightSibling;
private final T Data;
public LCRSNode(T data) {
Data = data;
}
public T getData() {
return Data;
}
public LCRSNode<T> getLeftChild() {
return LeftChild;
}
public LCRSNode<T> getRightSibling() {
return RightSibling;
}
public void setLeftChild(LCRSNode<T> leftChild) {
LeftChild = leftChild;
}
public void setRightSibling(LCRSNode<T> rightSibling) {
RightSibling = rightSibling;
}
}노드 생성시 데이터를 입력받고 LeftChild와 RightSibling은 자식 노드를 연결하는 연산에서 추가되기 때문에 null이 초기값이 되도록 하였다
자식 노드 연결하기
public void addChildNode(LCRSNode<T> parent, LCRSNode<T> child)
{
if (parent.getLeftChild() == null)
{
parent.setLeftChild(child);
}
else
{
LCRSNode<T> tempNode = parent.getLeftChild();
while (tempNode.getRightSibling() != null) {
tempNode = tempNode.getRightSibling();
}
tempNode.setRightSibling(child);
}
}매개변수로 부모 노드와 이 부모 노드에 연결할 자식 노드를 받는다.
그 후 먼저 부모 노드인 parent에게 자식 노드가 있는지 검사한다. 만약 없다면 자식이 없는 것이기 때문에 LeftChild에 자식으로 추가해준다.
자식 노드가 있다면 새로운 자식의 형제로 추가될 수 있도록 RightSibling에 추가해준다.
트리 출력
public void printTree(LCRSNode<T> node, int depth)
{
for (int i = 0; i < depth; i++)
System.out.print(" ");
System.out.println(node.getData());
if(node.getLeftChild() != null)
printTree(node.getLeftChild(),depth + 1);
if(node.getRightSibling() != null)
printTree(node.getRightSibling(),depth);
}트리 출력방식은 재귀호출을 통해 깊이 우선 탐색을 하여(사실 LeftChild 우선) LeftChilde가 없을 시에는 RightSibling을 탐색 후 출력하도록 한다.
예제소스
public class LCRSTreeTest
{
public static void main(String[] args)
{
LCRSNode<Character> Root = new LCRSNode<>('A');
LCRSNode<Character> B = new LCRSNode<>('B');
LCRSNode<Character> C = new LCRSNode<>('C');
LCRSNode<Character> D = new LCRSNode<>('D');
LCRSNode<Character> E = new LCRSNode<>('E');
LCRSNode<Character> F = new LCRSNode<>('F');
LCRSNode<Character> G = new LCRSNode<>('G');
LCRSNode<Character> H = new LCRSNode<>('H');
LCRSNode<Character> I = new LCRSNode<>('I');
LCRSNode<Character> J = new LCRSNode<>('J');
LCRSNode<Character> K = new LCRSNode<>('K');
LCRSTree<Character> tree = new LCRSTree<>();
tree.addChildNode(Root,B);
tree.addChildNode(B,C);
tree.addChildNode(B,D);
tree.addChildNode(D,E);
tree.addChildNode(D,F);
tree.addChildNode(Root,G);
tree.addChildNode(G,H);
tree.addChildNode(Root,I);
tree.addChildNode(I,J);
tree.addChildNode(J,K);
tree.printTree(Root, 0);
}
}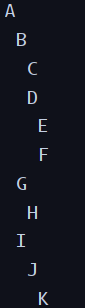
마무리
이렇게 트리의 기본적인 구조와 구현방식을 살펴보았다. 다음에는 현재 많이 쓰이는 이진트리에 대해 알아보겠다.
'CS > 자료구조' 카테고리의 다른 글
| 이진 트리(Binary Tree) 개념 및 구현 (0) | 2022.06.17 |
|---|---|
| 큐(Queue) 개념 및 구현 (0) | 2022.06.03 |
| 스택(Stack) 개념 및 구현 (0) | 2022.05.25 |
| 더블 링크드리스트(Doubly Linked List) 개념과 구현 (0) | 2022.05.20 |
| 링크드리스트(LinkedList) 개념 및 구현 (0) | 2022.05.20 |
